基本介紹
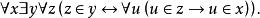冪集公理這個公理說明:“對於任何的x，存在著一個集合y，使y的元素是而且只會是x 的子集。”換句話說：給定任何集合x，有著一個集合P(x)，使得給定任何集合z，z 是P(x)的成員，若且唯若z 是x 的子集。通過外延公理可知，這個集合是唯一的。我們可以稱集合P(x)為x的冪集。所以這個公理的本質是：所有集合都有一個冪集。冪集公理一般被認為是無可爭議的，它或它的等價者出現在所有可替代的集合論的公理化中。冪集公理允許定義兩個集合X和Y的笛卡兒積：
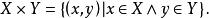冪集公理笛卡兒積為一個集合是因為
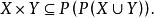冪集公理可以遞歸地定義集合的任何有限的蒐集的笛卡兒積：
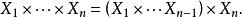冪集公理注意，在不包含冪集公理的克里普克—布萊特集合論中，笛卡兒積的存在性是可以證明的 。
相關性質定理
由外延公理知，B是唯一的，並稱B是A的冪集。因此有如下定義。
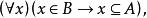冪集公理
冪集公理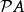
冪集公理
冪集公理定義1集合B是集合A的一個冪集，若且唯若 的冪集 記作 ，便有
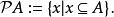冪集公理關於冪集的討論，從有限集合的冪集開始。為此，先定義有限集合。
定義2對於一個集合A，如果存在自然數n，使得A恰有n 個元，則稱A 是有限的。
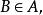冪集公理
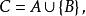冪集公理定理1若A是一個有限集合，且 令 則C的所有子集的個數恰是A 的所有子集的個數的二倍。
證明：因為對於A的每個子集，可加入B和不加人B這個元，這樣便得到C的所有子集，所以C的子集個數恰是A的子集個數的兩倍。
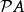冪集公理
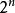冪集公理定理2對於自然數n，如果集合A恰有個n元，則 恰有 個元。
冪集公理
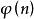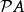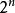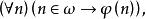冪集公理 冪集公理 冪集公理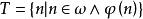
冪集公理
冪集公理證明：用:的歸納原理加以證明。對於n，設是命題：對任意集合A，若A有n個元，則有個元。本定理證明化為：也即要證：是個歸納集，因此，
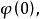冪集公理
冪集公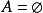理
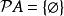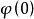冪集公理
冪集公理①證令，則，即2 =1故有成立。
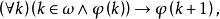冪集公理
冪集公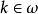理
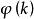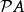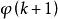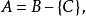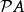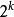冪集公理 冪集公理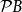
冪集公理
冪集公理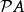 冪集公理
冪集公理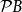
冪集公理 冪集公理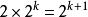 冪集公理
冪集公理②證設，且，即若A有k個元，則已知有2 個元。今證。設B有k+1個元的集合，C∈B且則A有k個元，故有個子集，由定理1知，有子集個數是的子集個數的二倍，即有個子集 。
下面給出冪集的一般性質的定理。
定理3
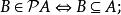冪集公理（1）
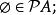冪集公理（2）
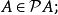冪集公理（3）
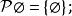冪集公理（4）
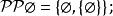冪集公理（5）
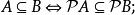冪集公理（6）
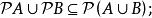冪集公理（7）
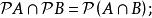冪集公理（8）
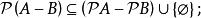冪集公理（9）
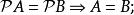冪集公理（10）
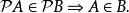冪集公理（11）
下面討論冪集與傳遞集的密切關係，首先給出如下定義。
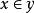冪集公理
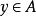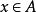冪集公理
冪集公理定義3對於集合A中任何集合x和y，若 且 ，則 ，稱A為傳遞集。
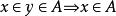冪集公理由定義可知， ，可見，要說明A是個傳遞集，只要用下面三種論述之一成立時，便可斷定A是傳遞集：
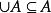冪集公理
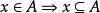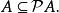冪集公理
冪集公理① ，② ，③
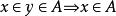冪集公理因為它們都等價於 這個性質。
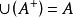冪集公理定理4對於傳遞集A，有 。
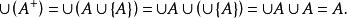冪集公理證明： 因為
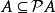冪集公理定理5集合A是傳遞集若且唯若 。
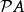冪集公理定理6集合A是一個傳遞集若且唯若 是傳遞集。
定理7每個自然數是個傳遞集。
冪集公理定理8集合 是個傳遞集 。
