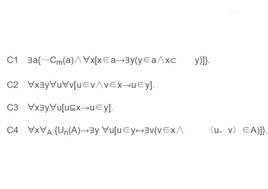基本介紹
集合存在性公理是GB系統的集合論公理,指GB系統中的第3組(即C組)公理,共有4條:
1.無窮公理,即無條件承認有一非空集a,對於a的每一元x,必有a的元y,使得x為y的真子集,因此,a的元必有無窮多。
2.並集公理,即斷言對任何集x,都存在著一集y,使得x的任何元的元都是y的元 。
3.冪集公理,指對任何集x,都有集合y存在,使得x的任一子集都是y的元。
4.替換公理,指對任何集合x和任何單值的A,總有集合y存在,此y恰由x的元經由單值二元關係A所產生的集組成。
其符號表達式依次為:
C1 ∃a{~C(a)∧ᗄx[x∈a→∃y(y∈a∧x⊂ y)]}.
C2 ᗄx∃yᗄuᗄv[u∈v∧v∈x→u∈y].
C3 ᗄx∃yᗄu[u⊆x→u∈y].
C4 ᗄxᗄ{U(A)→∃y ᗄu[u∈y↔∃v(v∈x∧ 〈u,v〉∈A)]}.
注意,由C1,C2,C3所決定的新集合併不惟一確定,又上述諸符號表達式中之C和U分別指空類和單值,亦即 :
C(X)→ᗄuᒣ(u∈X),
U(X)↔ᗄuᗄvᗄw[〈 〉∈X∧〈 〉∈X→v=w].
無窮公理
無窮公理(axiom of infinity)亦稱無限公理,是集合論的一條重要公理,由策梅洛(E.F.F.Zermelo)於1908年首先提出,該公理是斷言:存在無窮集合。對策梅洛這一公理的形式化有各種不同的方法,較為成功的有:
1.∃X(∃u(u∈X)∧(∀u∈X)
(∃v(v∈X∧u⊆v∧¬(v=u)).
2.存在一個遞歸集S:∃S(∅∈S∧(∀X∈S)[X∪{X}∈S]).遞歸集是無限集;反之,利用替換公理模式可從無限集的存在性推出遞歸集的存在性.
另外,1925年,塔爾斯基(A.Tarski)定義了T無限的概念:如果存在X⊆P(N),沒有極大元素,則稱N是T無限集,他證明了一個集合無限,若且唯若它是T無限的,因此無窮公理也可表述為:存在T無限集 。
並集公理
並集公理(axiom of union)是集合論的一條重要公理,由策梅洛(E.F.F.Zermelo)於1908年提出,該公理斷言:對任何集合X,存在X的所有元素的並集Y=∪X.這條公理可以形式化為:
 集合存在性公理
集合存在性公理∀X∃Y∀u(u∈Y∃z(z∈X∧u∈z)).
利用這條公理可以定義集合的並運算,例如,X∪Y=∪{X,Y},X∪Y∪Z=(X∪Y)∪Z.{a,b,c}={a,b}∪{c}等.也可以定義集合的包含關係:
 集合存在性公理
集合存在性公理X⊆Y∪{X,Y}=Y.
由於X⊆X∪Y,Y⊆X∪Y,所以,從並集公理可以得出包含公理:對任意兩集X與Y,存在同時以X,Y為子集的集合 。
冪集公理
冪集公理(axiom of power set)是集合論的一條重要公理,由策梅洛(E.F.F.Zermelo)於1908年首先提出,該公理斷言:對任何集合X,存在它的所有子集組成的集合(冪集)Y=P(X).這條公理可以形式化為∀X∃Y∀u(u∈Y↔∀v(v∈u→v∈X)).如果把∀v(v∈u→v∈X)記為u⊆X,表示u是X的子集,公理又可形式化為:∀X∃Y∀u(u∈Y↔u⊆X),從冪集公理得,X∈P(X)且¬(P(X)X),並可以定義集合論中一系列重要的概念,例如,集合的笛卡兒積、二元關係、二元關係的定義域、值域、域、n元關係、對應、映射、映射的限制、映射的擴張、運算、集上等價關係等.因為這些概念都有一個根本的出發點:對任何二集合X與Y,X×Y⊆P(P(X∪Y)),即X×Y是集合 。
替換公理
替換公理(axiom of replacement)亦稱置換公理,是集合論的一條重要公理,替換公理由弗倫克爾(A.A.Fraenkel)於1922年首先提出,該公理斷言:對任何集合論公式A(u,v)有
∀u∃v∀w(A(u,v)∧A(u,w)→v=w)→
∀X∃Y∀v(v∈Y↔(∃u∈X)A(u,v)).
這條公理指出,對於任何集合X與任何公式A(u,v)確定的映射f,映射的象f(X)是一個確定的集合,由於公式A(u,v)有無窮多個,每個具體的公式都確定一條公理,因此,弗倫克爾的公理實質上是一個公理模式,它包含了無窮多條公理。替換公理的引入,解決了某些ZF集合論其他公理不能解決的問題。有了這條公理,可以推得某種非常大的特殊集合,但是如果去掉無窮公理,由替換公理推不出無窮集的存在性.在ZF中,子集公理與空集公理可直接由替換公理推出.由替換公理與冪集公理可導出配對公理。
替換公理有下列各種等價形式:
1.若F是一個映射,則對任何集合A,F(A)是一個集合。
2.若F是一個映射,且定義域dom(F)是集合,則值域ran(F)也是集合。
3.若F是一個映射,則∀A∃f(F|A=f),下面的P,P,…,P是參變元。
4.對任何集合論公式φ(x,y,P,P,…,P)有∀x∃y∀z(φ(x,y,P,P,…,P)∧φ(x,z,P,P,…,P)→y=z)→∀X∃Y∀y(y∈Y↔(∃x∈X)φ(x,y,P,P,…,P)) 。