概念
全純映射是複流形之間的解析映射。設M,N分別是復m,n維複流形,f:M→N是連續映射。若對每一點p∈M,存在一個鄰域U,使得f在U內可用局部坐標函式表示成:
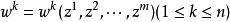 全純映射
全純映射其中ω都是全純函式,則稱f是全純映射。
映射
映射亦稱函式。數學的基本概念之一。也是一種特殊的關係。設G是從X到Y的關係,G的定義域D(G)為X,且對任何x∈X都有惟一的y∈Y滿足G(x,y),則稱G為從X到Y的映射。即關係G為映射時,應滿足下列兩個條件:
1.(x∈X)(y∈Y)(xGy).
2.(x∈X)(y∈Y)(z∈Y)((xGy∧xGz)→y=z).這個被x∈X所惟一確定的y∈Y,通常表示為y=f(x)(x∈X).f(x)滿足:
1) f(x)∈Y.
2) G(x,f(x))成立(x∈X).
3)z∈Y,G(x,z)→z=f(x).
關係G常使用另一些記號:f:X→Y或XY。f與G的關係是y=f(x)(x∈X),若且唯若G(x,y)成立。可取變域X中的不同元素為值的變元稱為自變元或自變數。同樣可取變域Y中的不同元素為值的變元稱為因變元或因變數。始集X稱為映射f的定義域。記為D(f)或dom(f)。終集Y稱為映射的陪域,記為C(f)或codom(f).Y中與X中的元素有關係G的元素的組合{y|x(x∈X∧y=f(x)∈Y)}稱為映射的值域,記為R(f)或ran(f)。當y=f(x)時,y稱為x的象,而x稱為y的原象。y的所有原象所成之集用f(y)表示。對於AX,所有A中元素的象的集合{y|x(x∈A∧y=f(x)∈Y)}或{f(x)|x∈A}稱為A的象。記為f(A)。對於BY,所有B中元素的原象的集合{x|x∈X∧y(y∈B∧y=f(x))}稱為B的原象。記為f(B)。顯然:f(A)=f(x),f(B)=f(y)。
流形
流形是一類特殊的連通、豪斯多夫仿緊的拓撲空間,在此空間每一點的鄰近預先建立了坐標系,使得任何兩個(局部)坐標系間的坐標變換都是連續的。n維流形的概念在18世紀法國數學家拉格朗日的力學研究中已有萌芽。19世紀中葉英國數學家凱萊(1843)、德國數學家格拉斯曼(1844,1861)、瑞士數學家施勒夫利(1852)分別論述了n維歐幾里得空間理論,把它視為n個實變數的連續統。1854年德國數學家黎曼在研究微分幾何時用歸納構造法給出一般n維流形的概念:n維流形是把無限多個(n-1)維流形按照一維流形方式放在一起而形成的,從此開始流形的拓撲結構及其局部理論的研究。法國數學家龐加萊在19世紀末把n維流形定義為一種連通的拓撲空間,其中每一點都具有和n維歐氏空間同胚的鄰域(被稱為龐加萊流形),從而開闢了組合拓撲學的道路。
對流形的深入研究集中在流形上的微分結構與組合結構的存在性、唯一性問題,微分結構與組合結構的關係,流形的各種意義下的分類等問題,20世紀50—60年代做出許多重要結果,近幾十年來出現有限維帶邊流形和無限維流形概念。流形理論在與其他拓撲理論的相互結合發展中也提出許多問題,其研究仍在繼續。
複流形
複流形是無支點黎曼曲面的推廣。設M為具有可數基的仿緊拓撲空間,且在M上有開覆蓋{U},使得對每個開集U,存在U到C中的域上的同胚映射φ,於是U中任給一點p,則:
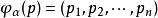 全純映射
全純映射稱為點p關於區圖(U,φ)之坐標。設對M中任一點q,若存在U,U使得q∈U∩U.記q關於(U,φ)之坐標為(x,x,…,x),關於(U,φ)之坐標為(y,y,…,y),則:
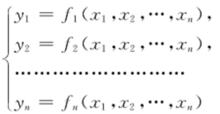 全純映射
全純映射為φ(U∩U)到φ(U∩U)上的全純同構,這時M稱為n維複流形。n維複流形為2n維實解析流形,反之不一定。
複流形和實流形概念的引進擴大了微分幾何和實分析的對象,產生了像大範圍分析那樣的學科一樣,複流形概念的引進,擴大了複分析的研究領域和產生像復幾何那樣的學科,其中緊複流形的研究成果較多。最簡單的緊複流形為緊黎曼面及n維復射影空間P 。
全純函式
亦稱解析函式或正則函式,是解析函式論的主要研究對象。對於定義於複平面上區域D內的復變數z的單值函式f(z),如果它在D內的每個點z的一個鄰域內都可以用z-z的冪級數表示,則稱f(z)在D內解析。外爾斯特拉斯(Weierstrass,K.(T.W.))從冪級數出發,建立了解析函式的級數理論。如果在D內的每個點z處,極限:
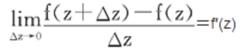 全純映射
全純映射(稱為函式f(z)在z點的導數)都存在,柯西(Cauchy,A.-L.)稱f(z)在D內是解析的。這兩個定義是等價的。函式f(z)=u(x,y)+iv(x,y),z=x+iy在D內解析的另一個等價條件是:u=u(x,y),v=v(x,y)在D內的每一個點z=x+iy處存在連續偏導數,並且滿足柯西-黎曼方程(或稱柯西-黎曼條件):
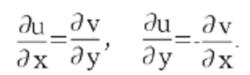 全純映射
全純映射這個條件有時簡稱C-R條件或稱達朗貝爾-歐拉條件。函式f(z)在區域D內解析的第四個等價條件是莫雷拉定理。
