簡介
多復變全純函式亦稱多復變解析函式,是多複變函數論研究的主要對象。
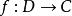 多復變全純函式
多復變全純函式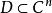 多復變全純函式
多復變全純函式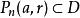 多復變全純函式
多復變全純函式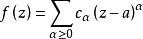 多復變全純函式
多復變全純函式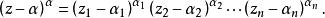 多復變全純函式
多復變全純函式設是定義在域上的函式,如果對α=(α,α,...,α)∈D,存在以a為中心,r為半徑的多圓柱,使得在P(a,r)中成立,就稱為f(z)在a點解析,這裡α=(α,α,...,α)是多重指標,α,α,...,α都取整數,α≥0表示α,α,...,α都取非負整數;而
如果f(z)在D中每點都解析,就稱f(z)在D上是全純的。
等價定義
D上的全純函式還有下面兩種等價定義:
1、D上的連續函式f(z)稱為是全純的,如果對每個j=1,2,...,n及每個固定的z,z,...,z,z,...,z,函式f(z,z,...,z,z,...,z)作為單復變數z的函式,在域D(z,z,...,z,z,...,z)={z∈C|(z,z,...,z,z,...,z)∈D}是全純的。
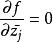 多復變全純函式
多復變全純函式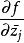 多復變全純函式
多復變全純函式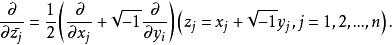 多復變全純函式
多復變全純函式2、D上的函式f(z)稱為是全純的,如果f(z)在D上連續,且對每個j=1,2,...,n,柯西-黎曼方程在D上成立,這裡偏微分運算元定義為
多複變函數論
數學中研究多個復變數的全純函式的性質和結構的分支學科,有時也稱多複分析。它雖然有著經典的單複變函數的淵源,但由於其特有的困難和複雜性,在研究的重點和方法上,都和單複變函數論有顯著的區別。
因為多復變全純函式的性質在很大程度上由定義區域的幾何和拓撲性質所制約,因此,其研究的重點經歷了一個由局部性質到整體性質的逐步的轉移。
