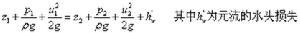理想流體運動微分方程的伯努利積分
恆定流動u=u(x、y、z) ,p=p(x、y、z),質量力以U(x、y、z)表示,理想流體運動微分方程沿流線積分,得:
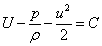
這個方程就稱為伯努利積分。該式表明,在有勢力作用下常密度理想流體恆定流動中同一條流線上的U-p/ρ-u^2/2值保持不變。一般情況下,積分常數C的值隨流線的不同而變化。
若流動是在重力場中,作質量力只有重力,所選z軸垂直向上,則質量力的勢函式U=-gz,代入上式,得
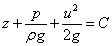
重力場中不可壓縮流體的伯努利積分式稱為伯努利方程。
元流伯努利方程的物理意義和幾何意義
1.物理意義元流的伯努利方程各項分別表示了單位重量流體的三種不同形式能力形式。z、p/ρg物理意義是單位重量流體具有的位能和壓能,z+p/ρg是單位重量流體具有的總勢能,u^2/2g是單位重量流體具有的動能。三項之和z+p/ρg+u^2/2g是單位重量流體具有的機械能。上式(2)表明,沿同一元流(同一流線),單位重量流體具有的機械能守恆。故伯努利方程也稱為能量方程。
2.幾何意義能量方程中的各項具有長度量綱,可以用水頭表示。z表示位置水頭,p/ρg是壓強水頭,u^2/2g是速度水頭,三項之和z+p/ρg+u^2/2g稱為總水頭。上式(2)表明,沿同一元流(同一流線)各斷面的總水頭是不變的。
實際粘性流體元流的伯努利方程
實際流體具有粘性,流動過程中因質點之間相對運動而產生流動阻力,克服阻力做功,使流體的一部分機械能不可逆地轉化為熱能散失,散失的能量稱為水頭損失。
根據能量守恆原理,便可得到粘性流體元流的伯努利方程,如下: