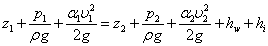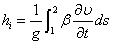總流伯努利方程
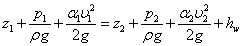
總流的伯努利方程適用條件:恆定流,質量力只有重力,不可壓縮流體,所取斷面為漸變流(兩斷面之間可以是急變流),兩斷面無分流和匯流(即流量沿程不變)。
總
流伯努利方程的水頭線
實際流體的總水頭線沿程單調下降,表示任意兩個斷面之間的水頭損失hw>0。下降的快慢用水力坡度J表示,J是單位流程內的水頭損失,為J=-dH/dL=dhw/dL。
對於理想流體J=0,故理想流體恆定流的總水頭線為一條水平直線;對於實際流體。J>0,總水頭線總是沿程下降的。
不可壓縮氣流的伯努利方程
公式及意義由於氣流的密度同外部空氣的密度是相同的數量級,在用相對壓強進行計算時,需要考慮外部大氣壓在不同高度的差值。下面為氣流伯努利方程:
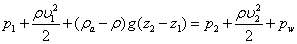
(ρa-ρ)g是單位體積氣體所受的有效浮力,(z2-z1)是氣體沿浮力方向升高的距離,(ρa-ρ)g(z2-z1)是1-1斷面相對於2-2斷面單位體積氣體的位能(稱為位壓),pw是壓強損失。
當氣流的密度與外界空氣的密度相同時或兩計算點的高度相同時,上式可以簡化為:
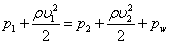
其中靜壓和動壓之和稱為總壓。
當氣流的密度遠大於外界空氣的密度時,此時相當於液體總流前一式中的ρa可忽略不計,認為各點的當地大氣壓相同,可以簡化為:
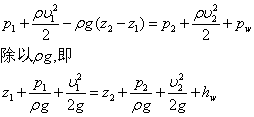
(1)動能修正係數
動能修正係數α為實際動能與按平均速度計算的動能的比值, α值反映了斷面速度分布的不均勻程度。由於氣體的動力黏度值較小,過流斷面速度梯度小,實際的氣流運動的速度分布比較均勻,接近於斷面平均流速。所以,氣體運動中的動能修正係數常常取1.0。
(2)氣流能量方程應採用壓強量綱
能量方程用於液體時,因液體中水頭概念很直觀具體,採用長度量綱很方便。但是氣體流動則不同,由於氣體重度γ很小,壓強一般比較大,水頭概念不明確。所以一般採用壓強量綱。
(3)氣流能量方程應採用絕對壓強
其原因是:方程中兩個過流斷面之間的高差比較大時,由於不同高度大氣壓強不同,而導致兩斷面相對壓強的起算基準不同。因此,將總流能量方程的兩端,直接代入該斷面處得相對壓強值進行計算,必定會產生誤差。
有能量輸入或輸出的伯努利方程
總流伯努利方程是在兩過流斷面間除水頭損失之外,再無能量輸入或輸出的條件下導出的。當兩過流斷面間有水泵、風機或水輪機等流體機械時,則存在機械能的輸入或輸出。在這種情況下,根據能量守恆原理,計入單位重量流體流經流體機械獲得或失去的機械能Hm,總流能量方程便擴展為有能量輸入或輸出的伯努利方程:
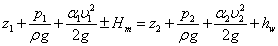
兩斷面間有分流或匯流的伯努利方程
恆定總流的伯努利方程是在兩過流斷面間無分流或匯流的條件下導出的,而實際的輸水、供氣管道,沿程大多都有分流或匯流。在這種情況下套用上下游斷面之間全部重量流體的能量守恆原理寫出能量方程。
非恆定總流伯努利方程
以上的總流的伯努利方程都是恆定總流,下面補充非恆定總流的伯努利方程。