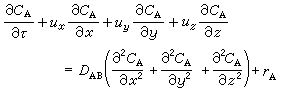對流擴散方程:對流擴散方程，表征流動系統質量傳遞規律的基本方程，求解此方 -百科知識中文網

對流擴散方程

對流擴散方程，表征流動系統質量傳遞規律的基本方程，求解此方程可得出濃度分布。此方程系通過對系統中某空間微元體進行物料衡算而得。對於雙組分系統,A組分流入某微元體的量，加上在此微元體內因化學反應生成的量，減去其流出量,即為此微元體中組分A的積累量。

對流擴散方程

對於雙組分系統,A組分流入某微元體的量，加上在此微元體內因化學反應生成的量，減去其流出量,即為此微元體中組分A的積累量。考慮到組分A進入和離開微元體均由擴散和對流兩種作用造成,而擴散通量是用斐克定律（見分子擴散）表述的，於是可得如下的對流擴散方程：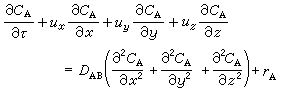

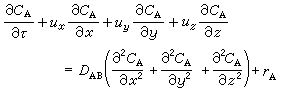
對流擴散方程

式中DAB為組分A在組分B中的分子擴散係數;rA為單位時間單位體積空間內因化學反應生成組分A的量;CA為組分A的質量濃度；τ為時間；ux、uy和uz分別為流速u的三個分量。對於僅有x方向的定態流動,且無化學反應生成組分A時，則對流擴散方程可簡化成為：

將濃度邊界層概念運用於傳質過程，可將二維對流擴散方程簡化，得到傳質邊界層方程：

上述方程表明，傳質與流動密切相關；只有解得速度分布之後，才能從對流擴散方程解得濃度分布，進而求得傳質通量。