水動力學
正文
研究液體運動的規律及其在工程中的套用，是水力學的一個分支。各種邊界所限制的流動空間，稱為流場，反映流場運動的物理量，統稱為運動要素。水動力學分析的目的，在於確定流場運動要素（速度和壓強）隨時間和空間位置而變化的函式關係式。水動力學通常以理想液體為分析對象。所謂理想液體，就是無粘滯性和無壓縮性的流體模型。這個模型是將實際液體在物理性質上加以簡化，以便於從理論上求得運動要素，然後再用實驗得出的結果加以修正，從而解決工程計算問題。
基本概念 恆定流動及非恆定流動 液體運動要素不隨時間而變的流動，稱為恆定流動。反之，稱為非恆定流動。
流線 流場中一條曲線，在同一時刻這條線上各流體質點的流速向量都與此線在該點相切。流線具有瞬時的概念。它由空間連續點在同一瞬時所組成。對於非恆定流，在不同時刻，流線具有不同的形狀。在恆定流中，由於空間點的流速不隨時間而變，流線的形狀將保持不變，流體質點將沿流線流動。流線是水力學分析的基本工具，在流場中繪出足夠的流線，就可形象地反映流動形態。
元流 連續流線組成封閉的管狀表面,稱為流管;流管內的液流，稱為流束；橫截面為無限小的流束，稱為元流。元流斷面上各點運動要素可以認為相等，常取為研究對象，進行力學分析。
總流 在固體邊界或大氣邊界內，如管壁內、河槽內、孔口管嘴和堰的周邊內無數元流的總和稱為總流。元流是總流的微分概念。所以水動力學的研究總是先研究元流，然後再推廣到總流。
過水斷面 與元流或總流各流線正交的橫斷面，稱為元流或總流的過水斷面。它可以是平面也可以是曲面，如果所有流線接近相互平行的直線，則過水斷面可視為平面，這段水流流動稱為漸變流動。
流量 單位時間經過某一過水斷面的液體體積稱為體積流量，簡稱流量，以Q表示。
斷面平均流速 總流過水斷面上各點流速的平均值，以v表示，v＝Q/A，式中A為過水斷面面積。以平均流速為研究對象，可將實際的以質點為對象的空間流動或平面流動用一維流動代替，這種簡化方法是水力學最基本的方法之一。
基本方程 連續性方程 在單位時間內，水流沿總流的一端流入的流體體積為v1A1，而沿另一端流出的流體體積為v2A2，從兩斷面之間流體質量不滅可證明：
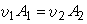(1)
伯努利方程 在恆定流場中任取一段元流，根據動能定理，運動液體的動能增量等於作用在該流段上各外力（重力和壓力）所作功的代數和，得出元流伯努利方程為
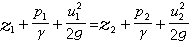(2)
如果要將理想液體恆定元流的伯努利方程，推廣到實際粘性液體的總流中，必須對(2)式作如下改變:①所研究流段的起始斷面和終了斷面應符合漸變流的條件；②u2/2ɡ應改為αv2/2ɡ，這是因為在實際液體總流中過水斷面上各點流速不等，所以將點流速u用平均流速v來代替;αv2/2ɡ為單位重量液體所具有的平均動能,α是動能修正係數,它是由於斷面上流速分布不均而引起的,其值與流速在斷面上的分布有關，對於紊流一般在1.05～1.1之間，為簡化計算可取 α等於1；③實際液體運動由於要克服摩擦阻力做功要消耗能量，所以要考慮能量損失,單位重量液體在流段間的平均能量損失用hl表示,稱為水頭損失（見水流阻力和水頭損失）。則 (2)式變為
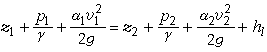(3)
動量方程 在總流中取兩斷面間的水流，根據動量定理，單位時間內流段的動量變化等於作用於該流段上的合外力，即：
(4)
一元非恆定流能量方程 設流場為理想液體非恆定流場，且密度 ρ為常數，將牛頓第二運動定律套用到所研究的元流段上，可得到理想液體非恆定元流的能量方程：
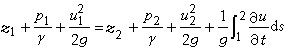(5)
是由於流動的非恆定性所造成,稱為慣性水頭;ds為流段的微元長度。 參考書目
V.Streeter，F.Wylie, Fluid Mechanics, McGraw-Hill，New York，1975.
