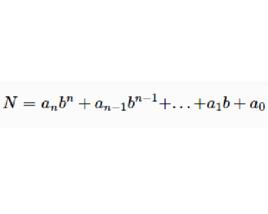基本介紹
定義
位值記數法是指按位值制來記數的方法，即一個數的大小，用一組有順序的數字來表示，每個數字所表示的大小，既取決於它本身的數值；又取決於它所在的位置。
羅馬數碼是一種非位值制記數法，而通常的進位制記數法，都是位值記數法。最早具有位值制思想的，是公元前二千年前後的古巴比倫人，但所用的是六十進制。在世界上，中國最先在商代(約公元前16、17世紀至約公元前1045年左右)，就已經使用十進制位值記數法了。戰國時(公元前4世紀)或更早，已經形成了採用完善的、包含空位(零)的十進位值制的籌算記數法(不過直到10世紀才普遍使用)。印度在6世紀末，才真正開始廣泛使用十進位值制。9世紀後，他們所用的十進位值制及數字元號——阿拉伯數字，逐步傳到阿拉伯及歐洲各國。
位值制
位值制也被稱為 位置制、 地位制，是在進位制的基礎上發展起來的。所謂位值制，就是同一數碼如果處在不同的位置( 數位)，就有不同的位置值(也叫 權)，因而所表示的數值也就不同，實際上，它表示所在位置相應一級“單位”的一定倍數，例如6，在個位表示6×1，在十位表示6×10，在百位表示6×100等。更嚴格地說，在選定進位制的基底b後，給出0， 1，2，……，b-1這b個數的寫法(數碼)，於是，任何一個自然數N， 均可以用某個以這些數碼為係數(可以重複) 的b的多項式表示出來：
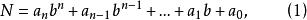位值制記數法
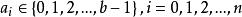位值制記數法其中， 。於是在“b進位值制”記數法中， 我們記N為
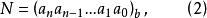位值制記數法
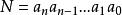位值制記數法顯然， 同一數碼寫在不同的位置上， 與之相應的b的冪次是不同的，因而這一數碼所表示的數值也就不同。此外， 當我們在特定的b進位值制系統中記數， 不至發生與其他基底的位值制記數法混淆時，便可把N的括弧和表示基底的腳碼b省略，直接寫成 。在常用的十進位值制和電子計算機用的二進位值制中人們正是這樣做的 。
十進制計數法
十進制(decimal system)是最常用的一種記數法，即以十為進位基數的位值制記數法，任何一個正整數都有一個且只有一個十進制表達式：
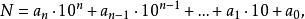位值制記數法
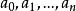位值制記數法
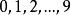位值制記數法
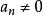位值制記數法
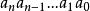位值制記數法其中 是 中的一個數， 。通常把N簡記為 ，小數也有十進制表示法。
發展歷程
在歷史上，較早發展起來的位值制記數系統有：巴比倫人的六十進位值制(不晚於公元前19世紀，參見“巴比倫數學”)；中國古代的十進位值制(不晚於公元前5世紀，參見“中國古代數學”)；瑪雅人的二十進位值制(約公元前的幾個世紀，參見“瑪雅數學”)；印度人的十進位值制(約公元5世紀前後，參見“印度古代數學”、“印度—阿拉伯數碼”) 。
在這裡， 我們把中國古代的十進位值制記數值產生的下限定在公元前5世紀，即春秋末年，因為在當時建立在十進位值制基礎上的算籌記數制度及其運算方法已經十分發達、完備而且普及了，實際上，十進位值制在中國產生的年代可能遠遠早於這個下限， 在約公元前14世紀至公元前11世紀的殷墟甲骨文中， 早已出現了像“三百又四十八”、“二千六百五十六人”這樣的記載，其特點是由一、二、三、…，九這9個數字與表示10的各個冪次的單字十、百、千、萬組合成一個複雜的數字， 在與10的各個冪次相應的每一級 (位)上，都是由一、二、……，九這9個數字之一與表示10的不同冪次的十、百、千、萬相乘而確定那一位上的數值時，這與前面表示b進位值制的多項式(1)在實質上是完全一致的，西方學者把這樣的記數系統稱為“乘法分群數系”，並認為位值制記數系統是乘法分群數系在邏輯上的必然產物。乘法分群數系與位值制記數系統的區別不僅在於前者必須把進位制基底b的備個冪次連同其係數一同寫出，還在於當某些係數是零時，前者就根本無需再提到這一項，而在後者(位值制)則必須在相應的位置上空位或補上一個零號。但是，另一方面， 甲骨文中的記載只是用當時的文字記述了數字運算的結果，而並沒有給出在實際運算中數字的表示法，這兩者是有明顯區別的。實際上，儘管十進位值制的算籌記數制度至遲在公元前5世紀已經十分普及， 但在由漢代到唐代形成的《算經十書》中，數字的文字敘述方式還是和甲骨文中的方式完全一樣，甚至在今天用漢字書寫數字時我們也同樣是這樣做的， 但這決不等同於在今天十進位值制仍未出現。
因此，英國著名科學史家李約瑟(J.Needham)曾經合理地推斷：“在西方後來所習見的‘印度數字’的背後，位值制早已在中國存在了兩千年。”雖然從文藝復興以來的歐洲學者幾百年來一直盛讚印度人發明了十進位值制這種極為簡捷優越的記數法， 但它最早是由中國人發明的卻是毫無疑問的 。
