例子
舉例明之,實數域並非代數閉域,因為下列實係數多項式無實根:
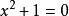 代數閉域
代數閉域 代數閉域
代數閉域同理可證有理數域非代數閉域。此外,有限域也不是代數閉域,因為若列出 F的所有元素,則下列多項式在F中沒有根:
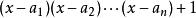 代數閉域
代數閉域反之,複數域則是代數閉域;這是代數基本定理的內容。另一個代數閉域之例子是代數數域。
等價的刻劃
給定一個域 F,其代數封閉性與下列每一個性質等價:
不可約多項式若且唯若一次多項式
域 F是代數閉域,若且唯若環 F[ x]中的不可約多項式是而且只能是一次多項式。
“一次多項式是不可約的”的斷言對於任何域都是正確的。如果 F是代數閉域, p( x)是 F[ x]的一個不可約多項式,那么它有某個根 a,因此 p( x)是 x − a的一個倍數。由於 p( x)是不可約的,這意味著對於某個 k ∈ F \ {0},有 p( x) = k( x − a)。另一方面,如果 F不是代數閉域,那么存在 F[ x]內的某個非常數多項式 p( x)在 F內沒有根。設 q( x)為 p( x)的某個不可約因子。由於 p( x)在 F內沒有根,因此 q( x)在 F內也沒有根。所以, q( x)的次數大於一,因為每一個一次多項式在 F內都有一個根。
每一個多項式都是一次多項式的乘積
域 F是代數閉域,若且唯若每一個係數位於次數 F內的 n ≥ 1的多項式 p( x)都可以分解成線性因子。也就是說,存在域 F的元素 k, x1, x2, ……, xn,使得 p( x) = k( x − x1)( x − x2) ··· ( x − xn)。
如果 F具有這個性質,那么顯然 F[ x]內的每一個非常數多項式在 F內都有根;也就是說, F是代數閉域。另一方面,如果 F是代數閉域,那么根據前一個性質,以及對於任何域 K,任何 K[ x]內的多項式都可以寫成不可約多項式的乘積,推出這個性質對 F成立。
Fn的每一個自同態都有特徵向量
域 F是代數閉域,若且唯若對於每一個自然數 n,任何從 F到它本身的線性映射都有某個特徵向量。
F^n的自同態具有特徵向量,若且唯若它的特徵多項式具有某個根。因此,如果 F是代數閉域,每一個 F^n的自同態都有特徵向量。另一方面,如果每一個 F^n的自同態都有特徵向量,設 p( x)為 F[ x]的一個元素。除以它的首項係數,我們便得到了另外一個多項式 q( x),它有根若且唯若 p( x)有根。但如果 q( x) = x^n+ an-1 x^n-1+ ··· + a0,那么 q( x)是以下友矩陣的特徵多項式:
0 0 0……0 -a01 0 0……0 -a10 1 0……0 -a2
有理表達式的分解
域 F是代數閉域,若且唯若每一個係數位於 F內的一元有理函式都可以寫成一個多項式函式與若干個形為 a/( x − b)^n的有理函式之和,其中 n是自然數, a和 b是 F的元素。
如果 F是代數閉域,那么由於 F[ x]內的不可約多項式都是一次的,根據部分分式分解的定理,以上的性質成立。
而另一方面,假設以上的性質對於域 F成立。設 p( x)為 F[ x]內的一個不可約元素。那么有理函式1/ p可以寫成多項式函式 q與若干個形為 a/( x − b)^n的有理函式之和。因此,有理表達式
可以寫成兩個多項式的商,其中分母是一次多項式的乘積。由於 p( x)是不可約的,它一定能整除這個乘積,因此它也一定是一個一次多項式。
代數閉包
設為代數擴張,且 E是代數閉域,則稱 E是 F的一個 代數閉包。可以視之為包含 F的最小的代數閉域。
若我們承認佐恩引理(或其任一等價陳述),則任何域都有代數閉包。設 E, E'為任兩個 F的代數閉包,則存在環同構使得σ | F = id F;代數閉包在此意義上是唯一的,通常記作 F 或。

