簡介
在數學及其相關領域中,一個對象具有 完備性,即它不需要添加任何其他元素,這個對象也可稱為 完備的或 完全的。更精確地,可以從多個不同的角度來描述這個定義,同時可以引入 完備化這個概念。但是在不同的領域中,“完備”也有不同的含義,特別是在某些領域中,“完備化”的過程並不稱為“完備化”,另有其他的表述,請參考代數閉域、緊化或哥德爾不完備定理。
一個度量空間或一致空間被稱為“完備的”,如果其中的任何柯西列都收斂,請參看完備空間。
在泛函分析中,一個拓撲向量空間V的子集S被稱為是 完全的,如果S的擴張在V中是稠密的。如果V是可分空間,那么也可以導出V中的任何向量都可以被寫成S中元素的(有限或無限的)線性組合。更特殊地,在希爾伯特空間中(或者略一般地,線上性內積空間(inner product space)中),一組標準正交基就是一個完全而且正交的集合。
一個測度空間是 完全的,如果它的任何零測集(null set)的任何子集都是可測的。請查看完全測度空間(complete measure)。
在統計學中,一個統計量被稱完全的,或完備的,如果不存在由其構造的非平凡的0的無偏估計量(estimator)。
在圖論中,一個圖被稱為 完全的,如果這個圖是無向圖,並且任何兩個頂點之間都恰有一條邊連線。
在範疇論,一個範疇C被稱為 完備的,如果任何一個從小範疇到C的函子都有極限。而它被稱為 上完備的,如果任何函子都有一個上極限。請查看範疇論中的極限定義。
在序理論和相關的領域中,如格和疇(域理論)中, 全序性(completeness)一般是指對於偏序集存在某個特定的上確界或下確界。值得特別注意的是,這個概念在特定的情況下也套用於完全布爾代數,完全格和完全偏序。並且一個有序域被稱為 完全的,如果它的任何在這個域中有上界的非空子集,都有一個在這個域中的最小上界;注意這個定義與序理論中的完全有界性(bounded complete)有細小的差別。在同構的意義下,有且僅有一個完全有序域,即實數。
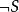 完全性
完全性在數理邏輯,一個理論被稱為 完備的,如果對於其語言中的任何一個句子S,這個理論包括且僅包括S或。一個系統是 相容的,如果不存在同時P和非P的證明。哥德爾不完備定理證明了,包含皮亞諾公理的所有公理系統都是不可能既完備又相容的。下面還有一些邏輯中關於完備性的定義。
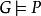 完全性
完全性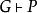 完全性
完全性在證明論和相關的數理邏輯的領域中,一個形式的演算相對於一個特定的邏輯(即相對於它的語義)是 完備的,如果任何由一組前提Q根據語義導出的陳述S,都可以從這組前提出發利用這個演算語法地導出。形式地說,導出。一階邏輯在這個意義下是完備的。特別地,所有邏輯的重言式都可以被證明。即使在經典邏輯中,這與前述的完備性是不同的(即一個陳述和否定陳述對於這個邏輯而言不可能是重言式)。相反的概念被稱為可靠性(soundness)。
在計算複雜度理論中,一個問題P對於一個複雜度類C,在某個給定類型的歸約下是 完全的(完備 (複雜度)),如果P在C中,並且C中的任何問題利用該歸約都可以化歸到P。例如,NP完全問題在NP類和多項式時間和多對一歸約的意義下是完全的。
參見
•完備空間
•緊化
•哥德爾不完備定理
•代數閉域
•完全測度空間
•完全布爾代數
•完備 (複雜度)
