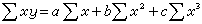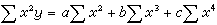代數穩定判據

簡介

根據系統特徵多項式的係數直接判斷系統穩定性的判據。系統的特徵多項式就是系統傳遞函式的分母多項式，它是復變數s的一個代數多項式,使這一多項式為零而求得的s值稱為特徵多項式的根。代數穩定判據只適用於線性定常系統（見線性系統、定常系統）且其特徵多項式能給出的情況。線性定常系統穩定的充分必要條件，是其特徵多項式的根均具有負實部，亦即均位於不包含虛軸的左半s複數平面內。代數穩定判據的優點是可以避免求根的複雜過程，直接根據多項式的係數的一些代數運算，來判定系統是否滿足上述穩定條件。
必要條件　若系統的特徵多項式為

其中a0，a1，…，an均為實數,則系統為穩定的必要條件是係數a0，a1，…，an均為正數。
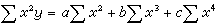
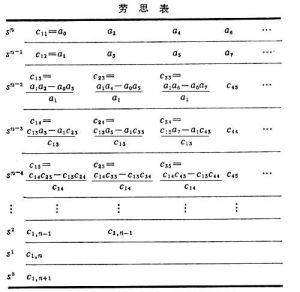
勞思判據　1875年英國數學家E.J.勞思所建立，根據D(s)的係數組成如下的勞思表。

代數穩定判據

系統為穩定的充分必要條件是勞思表的第一列元素C11、C12、C1n、C1n+1均為正數。
胡爾維茨判據　1895年德國數學家A.胡爾維茨所建立。根據D(s)的係數組成如下的n×n胡爾維茨矩陣：

其中下標指數大於 n的元均用零代替。系統為穩定的充分必要條件是矩陣H的一切順序主子式和a0均為正數，即△0=a0>0,△1=a1>0,△2=a1a2-a0a3>0,…,△n=|H|>0。其中│H│表示矩陣H的行列式。理論研究表明，胡爾維茨判據實質上與勞思判據是完全等價的。

套用

除了判斷系統的穩定性，代數穩定判據尚可用於：①確定不穩定系統特徵多項式的正實部根的數目：它等於勞思表中第一列的各係數符號的改變次數。②判斷系統是否具有所期望的衰減度:設期望衰減度為e-αt(α >0)；則取s=λ-α 並代入D(s),可得出以λ為待定量的新多項式β(λ)。對β(λ)運用代數穩定判據，如果穩定就意味著系統具有期望的衰減度，否則就不具有期望衰減度。③建立參數穩定域：對D(s)中包含的一個或幾個可變動係數，通過套用代數穩定判據可確定出系統為穩定時的係數範圍，由此可構成參數穩定域。