定義
假若勞斯陣列表中第一列係數均為正數，則該系統是穩定的，即特徵方程所有的根均位於根平面的左半平面。假若第一列係數有負數，則第一列係數符號的改變次數等於在右半平面上根的個數。
套用
相對穩定性
勞斯判據不僅可以判別系統穩定不穩定，即系統的絕對穩定性，而且也可檢驗系統是否有一定的穩定裕量，即相對穩定性。另外勞斯判據還可用來分析系統參數對穩定性的影響和鑑別延滯系統的穩定性。
求虛根
在根軌跡分析法中會遇到求根軌跡與虛軸交點的問題，即求閉環特徵方程的虛根的問題。可以藉助列寫勞斯表來解決。具體方法為：當勞斯表s 行係數等於0時，閉環特徵方程出現共軛虛根。令s 行係數等於0，則得根軌跡增益，再根據s 行的係數寫出輔助方程（形式為as +b=0）求得共軛虛根。
勞斯列表操作步驟
求特徵方程
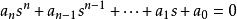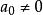勞斯判據
勞斯判據寫出線性系統的特徵方程，式中的係數為實數。設，即排除存在零根的情況。
觀察特徵方程係數
特徵方程中所有係數都存在並且均大於0，這是系統穩定的必要條件。因為任意個只包含正係數的一次和二次因子的乘積，必然也是一個具有正係數的多項式，所以，特徵方程缺項或具有負的係數項，系統便是不穩定的。
編制勞斯計算表
如果係數都是正數，那么按照下面的方式編制勞斯計算表。
勞斯陣的前兩行由特徵方程的係數組成：第一行由第1，3，5，…項係數組成，第二行由第2，4，6，…項係數組成。以下各行係數由下列（如下圖）公式計算。
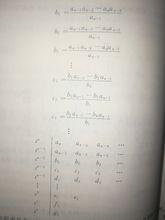勞斯表判定
特徵方程中，實部為正數的根的個數等於勞斯表的第一列元素符號改變的次數。因此，系統穩定的充分必要條件是：特徵方程的全部係數都是正數，並且勞斯表的第一列元素都是正數。
