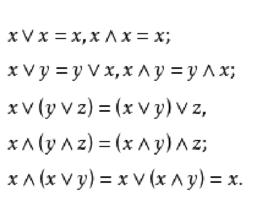關於格的交運算
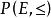 交運算
交運算 交運算
交運算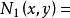 交運算
交運算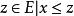 交運算
交運算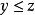 交運算
交運算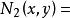 交運算
交運算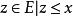 交運算
交運算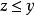 交運算
交運算 交運算
交運算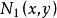 交運算
交運算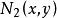 交運算
交運算 交運算
交運算 交運算
交運算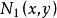 交運算
交運算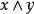 交運算
交運算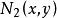 交運算
交運算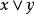 交運算
交運算格(lattice)是一類代數結構,它是建立在偏序集之上的,由E的任意元素構造的如下兩個集合{且}及{且},它們作為P的子集均仍為偏序集,一般不一定有最小元或最大元。若對P的任意元素,均有 最小元,均有 最大元,則稱P為 格,並記為。在格上,把和其最小元的對應關係視為一類二元運算,稱為x和y的 交,記為,對稱地,把和其最大元的對應關係視為x和y的結,記為。它們是格上最基本的運算,這兩類運算滿足:
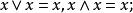 交運算
交運算1.同一律:
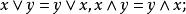 交運算
交運算2.交換律:
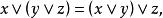 交運算
交運算3.結合律:
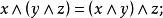 交運算
交運算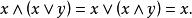 交運算
交運算4.吸收律:
 交運算
交運算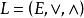 交運算
交運算其中和z均為E的任意元素,因此格又可視為滿足上述四條規律的代數結構。
 交運算
交運算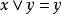 交運算
交運算 交運算
交運算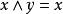 交運算
交運算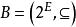 交運算
交運算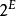 交運算
交運算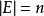 交運算
交運算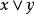 交運算
交運算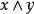 交運算
交運算 交運算
交運算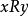 交運算
交運算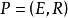 交運算
交運算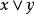 交運算
交運算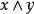 交運算
交運算雖然格的理論建立較晚,大約在20世紀30年代左右,但是很快就在解決序集問題和組合問題及代數問題中迅速發展,成為有關研究的有效理論基礎,格理論伴隨擬陣理論的發展就是一個明顯的例證,與一般具有序特徵的代數結構不同的是,格中元素的序特徵不是外在的,而是內在的,這是由於它們的序關係完全可以等價地由格的內在運算來刻畫:若且唯若或者若且唯若,這也反映了格的交運算與結運算的對稱性。有一些重要的格的例子。例如,格,這裡為E的所有子集的構成的集族,而,其上的結運算為集x和集y的並集,交運算為集x和集y的交集。又如,若自然數n的所有正整除數組成集合為E,E的元素有序關係若且唯若x能整除y,則偏序集為格,為x和y的最低公倍數,為x和y的最大公約數 。
集合的交運算
定義
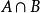 交運算
交運算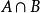 交運算
交運算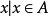 交運算
交運算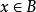 交運算
交運算對於任意兩個集合A、B,由所有既屬於A又屬於B的元素構成的集合,稱作A與B的 交集,記作。即:={且}。
舉例說明
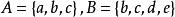 交運算
交運算例如,,則
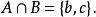 交運算
交運算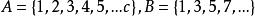 交運算
交運算又如,,則
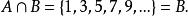 交運算
交運算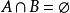 交運算
交運算如果集合
,也就是說集合A和B沒有公共元素,則稱A、B不相交。例如:
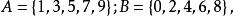 交運算
交運算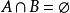 交運算
交運算那么,即A、B不相交 。
圖形表示
 交運算
交運算 交運算
交運算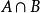 交運算
交運算集合之間的運算可以用文氏(John Venn英國數學家,1834-1923)圖形象地表示。如圖1所示,用平面上的矩形表示全集。用矩形內的圓表示中的任一集合。圖中陰影部分為。
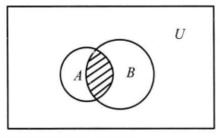 圖1 集合的交運算
圖1 集合的交運算由集合交運算的定義可知,交運算有以下性質:
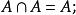 交運算
交運算(1) 冪等律:
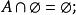 交運算
交運算(2)同一律:
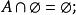 交運算
交運算(3)零律:
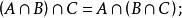 交運算
交運算(4)結合律:
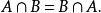 交運算
交運算(5)交換律:
類似地,結合律可以用歸納法推廣到有限個集合的情況,記
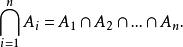 交運算
交運算