概念
集合運算是實體造型系統中非常重要的模組，也是一種非常有效的構造形體的方法。從一維幾何元素到三維幾何元素，人們針對不同的情況和套用要求，提出了不少集合運算算法。
在早期的造型系統中，處理的對象是正則形體，因此定義了正則形體集合運算，來保證正則形體在集合運算下是封閉的。在非正則形體造型中，參與集合運算的形體可以是體、面、邊、點，運算的結果也是這些形體，這就要求集合運算算法中能統一處理這些不同維數的形體，因此需要引入非正則形體運算。
1、正則集與正則集合運算運算元
Tilove根據點集拓撲學的原理，給出了正則集的定義。認為正則的幾何形體是由其內部點的閉包構成，即由內部點和邊界兩部分組成。對於幾何造型中的形體，規定正則形體是三維歐氏空間中的正則集合，因此可以將正則幾何形體描述如下：
主要類型
設G是三維歐氏空間R3中的一個有界區域，且G=bG∪iG，其中bG是G的n－1維邊界，iG是G的內部。G的補空間cG稱為G的外部，此時正則形體G需滿足：
1)bG將iG和cG分為兩個互不連通的子空間；
2)bG中的任意一點可以使iG和bG連通；
3)bG中任一點存在切平面，其法矢指向cG子空間
4)bG是二維流形。
對於正則形體集合，可以定義正則集合運算元。設是集合運算運算元（交、並或差），如果R3中任意兩個正則形體A、B作集合運算：
R=AB
運算結果R仍是R3中的正則形體，則稱為正則集合運算元，正則並、正則交、正則差分別記為∪*，∩*、-* 。
分類
幾何造型中的集合運算實質上是對集合中的成員進行分類的問題，Tilove給出了集合成員分類問題的定義及判定方法。
Tilove對分類問題的定義為：設S為待分類元素組成的集合，G為一正則集合，則S相對於G的成員分類函式為：
C(S,G)={S in G，S out G，S on G}， （3-2-1）
其中，
S in G=S∩iG，
S out G=S∩cG，
S on G=S∩bG，
如果S是形體的表面，G是一正則形體，則定義S相對於G的分類函式時，需考慮S的法向量。記-S為S的反向面。形體表面S上一點P相對於外側的法向量為NP(S)，相反方向的法向量為- NP(S)，則（3-2-1）式中S on G可分為兩種情況：
S on G ={S shared(bG)，S shared(-bG)}，
其中，
S shared(bG)={P|P∈S，P∈bG，NP(S)=NP(bG)},
S shared(-bG)={P|P∈S，P∈bG，NP(S)=-NP(bG)}。
於是，S相對於G的分類函式C(S,G)可寫為：
C(S,G)={S in G，S out G，S shared(bG)，S shared(-bG)}。
由此，正則集合運算定義的形體邊界可表達為：
b(A∪B)={bA out B，bB out A，bA shared(bB)}，
b(A∩B)={bA in B，bB in A，bA shared(bB)}，
b(A-B)={bA out B，-(bB in A)，bA shared(-bB)}。
3．集合運算算法
正則集合運算與非正則形體運算的區別在於增加了正則化處理步驟。下面，我們給出一個非正則形體的集合運算算法。
假定參與集合運算的形體為A和B，運算的結果形體C=AB，其中集合運算符為通常的集合運算並、交、差（È 、Ç 、- ）。
對於一個非正則形體L，可以將其分解為L=L3ÈL2ÈL1ÈL0，其中L3為R3中的正則閉集之並，存在面表、邊表、點表等拓撲元素。L2是懸面集，存在邊表和點表。L1是懸邊集，只有端點。L0是孤立點集。
集合運算整個算法包括了以下幾部分：
(1)求交：參與運算的一個形體的各拓撲元素求交，求交的順序採用低維元素向高維元素進行。用求交結果產生的新元素（維數低於參與求交的元素）對求交元素進行劃分，形成一些子元素。這種經過求交步驟之後，每一形體產生的子拓撲元素的整體相對於另一形體有外部、內部、邊界上的分類關係。
2)成環：由求交得到的交線將原形體的面進行分割，形成一些新的面環。再加上原形體的懸邊、懸點經求交後得到的各子拓撲元素，形成一拓撲元素生成集。
(3)分類：對形成的拓撲元素生成集中的每一拓撲元素，取其上的一個代表點，根據點/體分類的原則，決定該點相對於另一形體的位置關係，同時考慮該點代表的拓撲元素的類型（即其維數），來決定該拓撲元素相對於另一形體的分類關係。
(4)取捨：根據拓撲元素的類型及其相對另一形體的分類關係，按照集合運算的運算符要求，要決定拓撲元素是保留還是捨去；保留的拓撲元素形成一個保留集。
(5)合併：對保留集中同類型可合併的拓撲元素進行合併，包括面環的合併和邊的合併。
(6)拼接：以拓撲元素的共享邊界作為其連線標誌，按照從高維到低維的順序，收集分類後保留的拓撲元素，形成結果形體的邊界表示數據結構 。
集合的運算
並
主條目：並集
兩個集合可以相"加"。A和B的 並集是將A和B的元素放到一起構成的新集合。
定義
給定集合A，B，定義運算∪如下：A∪B = {e|e∈A 或 e∈B}。A∪B稱為A和B的 並集。
A 和 B 的並集
示例
•{1, 2}∪{紅色, 白色} = {1, 2, 紅色, 白色}
•{1, 2, 綠色}∪{紅色, 白色, 綠色} = {1, 2, 紅色, 白色, 綠色}
•{1, 2}∪{1, 2} = {1, 2}
基本性質
作為集合間的二元運算，∪運算具有以下性質。
交換律：A∪B = B∪A；
結合律：(A∪B)∪C = A∪(B∪C)；
冪等律：A∪A = A；
集合運算 集合運算麼元：∀集合A，A∪ = A；（是∪運算的麼元）。
交
主條目：交集
一個新的集合也可以通過兩個集合"共"有的元素來構造。 A和 B的 交集，寫作 A∩ B，是既屬於 A的、又屬於 B的所有元素組成的集合。
若 A∩ B={\displaystyle \varnothing }，則 A和 B稱作 不相交。
A 和 B 的交集
定義
給定集合A，B，定義運算∩如下：A∩B = {e|e∈A 且 e∈B}。A∩B稱為A和B的 交集。
基本性質
作為集合間的二元運算，∩運算具有以下性質。
•交換律：A∩B = B∩A；
•結合律：(A∩B)∩C = A∩(B∩C)；
•冪等律：A∩A = A；
集合運算 集合運算 集合運算空集合：∀集合A，A∩ =；（是∩運算的空集合）。
其它性質還有：
•A⊆B ⇒ A∩B = A
示例
集合運算{1, 2}∩{紅色, 白色} =
{1, 2, 綠色}∩{紅色, 白色, 綠色} = {綠色}
{1, 2}∩{1, 2} = {1, 2}
差
主條目：差集
兩個集合也可以相"減"。 A在 B中的 相對補集，寫作 B− A，是屬於 B的、但不屬於 A的所有元素組成的集合。
在特定情況下，所討論的所有集合是一個給定的全集 U的子集。這樣， U− A稱作 A的 絕對補集，或簡稱 補集（余集），寫作 A′或 CA。
補集可以看作兩個集合相減，有時也稱作 差集。
定義
集合運算給定集合A，B，定義運算-如下：A - B = {e|e∈A 且。A - B稱為B對於A的 差集， 相對補集或 相對余集。
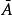集合運算在上下文確定了 全集U時，對於U的某個子集A，一般稱U - A為A（對於U）的 補集或 余集，通常記為A'或，也有記為CA的。
基本性質
作為集合間的二元運算，- 運算有如下基本性質：
集合運算A - A =；
集合運算 集合運算右麼元：∀集合A，A - = A；（是 - 運算的右麼元）。
集合運算 集合運算 集合運算左零元：∀集合A，- A =；（是 - 運算的左零元）。
示例
{1, 2}−{紅色, 白色} = {1, 2}
{1, 2, 綠色}−{紅色, 白色, 綠色} = {1, 2}
集合運算{1, 2}−{1, 2} =
若 U是整數集，則奇數的補集是偶數
對稱差
主條目：對稱差
定義
給定集合A，B，定義 對稱差運算△如下：A△B = (A-B)∪(B-A)。
基本性質
作為集合間的二元運算，△運算具有如下基本性質：
交換律：A△B = B△A；
結合律：(A△B)△C = A△(B△C)；
集合運算 集合運算麼元：∀集合A，A△= A；（是△運算的麼元）。
集合運算逆元：A△A =；
