發展歷史
交流電 早期的成品由尼古拉·特斯拉、麥可·法拉第與波利特·皮克西等人開發出來。其中，波利特·皮克西Hippolyte Pixii於1832年基於麥可·法拉第Michael Faraday的原理製造了第一台交流電機。
1882年，英國電工詹姆斯·戈登建造了大型雙相交流發電機。第一代開爾文男爵威廉·湯姆森（William Thomson, 1st Baron Kelvin，1824年6月26日－1907年12月17日）與塞巴斯蒂安·費蘭蒂Sebastian Ziani de Ferranti 開發早期交流發電機，頻率介於100赫茲至300赫茲之間。
1891年，尼古拉·特斯拉Nikola Tesla取得了“高頻率”（15,000赫茲）交流發電機的專利。
1891年後，多相交流發電機被用來供應電流，此後的交流發電機的交流電流頻率通常設計在16赫茲至100赫茲間，搭配弧光燈、白熾燈或電動機使用。
簡介
交流電（英語：Alternating Current，簡寫AC）是指大小和方向都發生周期性變化的電流，因為周期電流在一個周期內的運行平均值為零，稱為交變電流或簡稱交流電。不同於方向不隨時間發生改變的直流電。
通常波形為正弦曲線。交流電可以有效傳輸電力。但實際上還有套用其他的波形，例如三角形波、正方形波。生活中使用的市電就是具有正弦波形的交流電。
發明最早交流發電機的是美籍塞爾維亞裔科學家尼古拉·特斯拉。
以正弦交流電套用最為廣泛，且其他非正弦交流電一般都可以經過數學處理後，化成為正弦交流電的疊加。正弦電流（又稱簡諧電流），是時間的簡諧函式。
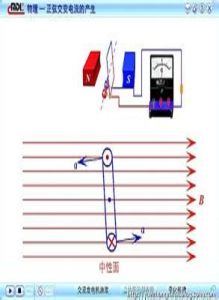
當閉合線圈在勻強磁場中繞垂直於磁場的軸勻速轉動時，線圈裡就產生大小和方向作周期性改變的正弦交流電。
中國通常使用的交流電，一般頻率是50Hz。
我們常見的電燈、電動機等用的電都是交流電。在實用中，交流電用符號"~"表示。
電流隨時間的變化規律，由此看出：正弦交流電三個要素：最大值（峰值）、周期（頻率或角頻率）和相位（初相位）。交流電所要討論的基本問題是電路中的電流、電壓關係以及功率（或能量）的分配問題。由於交流電具有隨時間變化的特點，因此產生了一系列區別於直流電路的特性。在交流電路中使用的元件不僅有電阻，而且有電容元件和電感元件，使用的元件多了，現象和規律就複雜了。但基本遵循安培定律等基本法則。是高中電學的的考點和難點。
根據傅立葉級數的原理，周期函式都可以展開為以正弦函式、餘弦函式組成的無窮級數，任何非簡諧的交流電也可以分解為一系列簡諧正餘弦交流電的合成。
產生和套用
交流電的來源大致有兩類，一類是由機械振動或其他非電信號轉換為電振盪，如傳聲器將聲音變為電振盪，壓電晶體把機械振動變為電振盪等，另一類則是交流發電機或電子振盪器，作為能源使用的都是屬於後一類型。
電力網中所用的交流電源都是利用電磁感應的原理製成的,稱為交流發電機。將一個線圈放在永久磁鐵(或電磁鐵）的磁場中鏇轉，則穿過線圈的磁通Ф 隨時間變動,因而將產生感應電動勢e=-dФ/dt 。如果線圈的鏇轉是勻速的，且角速率為ω，則感應電動勢就是周期的,其頻率f=ω/2π，而ω=2πf常稱之為角頻率。由於線圈鏇轉一周后其中磁通Ф的累積變動量等於零,故感應電動勢在一周期內的平均值也等於零，即電動勢是交變的。通常這種交變電動勢通過安裝在鏇轉軸上的兩個導電滑環用兩個電刷引出，若接通外電路，則在外電路中獲得頻率為f的交流電。為了獲得固定頻率的交流電,這種發電機的轉速必須是固定不變的，因此被稱為同步發電機。這種將機械能轉換為電能的裝置產生交流電，由於受到機械結構強度的限制，其轉速不能太高，因此頻率也就不可能很高,一般限於10000赫以下。為了獲得更高頻率的交流電源，可以採用電子振盪器。廣播電台、高頻感應加熱、電磁振動台、聲吶等裝置上所需用的較高頻率交流電源就屬這一類（見電磁振盪和電諧振）。
在M.法拉第1831年發現電磁感應現象後第二年，第一個最簡單的交流發電機就已問世，然而交流電開始得到廣泛套用還是在19世紀80年代以後，那時相繼發明了變壓器、三相制、鏇轉磁場和異步電動機；交流電路理論也隨著這些套用的需要而逐步建立，例如用相量表示正弦量的方法就是1893年C.P.施泰因梅茨提出的。1907年三極真空管的發明，為產生更高頻率的交流電及其在無線電方面的套用提供了條件。
目前，在動力方面,絕大部分電力網都是交流的,因為交流電可以方便地變換電壓；交流電機在結構上也比直流電機簡單；在需要直流的地方還可以很方便地採用電子整流裝置。中國1980年在東北建立的超高壓輸變電線路就是用的50萬伏交流電。
在信息傳輸方面也時常用到交流電，例如載波通信的載波電流就是交流電。
交流電路
當電路中通過交流電時，電路周圍與電路相關聯的磁通也隨著交變，從而在電路的各個部分感應電動勢e=-dФ/dt。另外，電路中的各個部分還存在著與電壓相關聯的電荷,其量值隨電壓的交變而交變,這些交變著的電荷就形成導線中的充放電電流 i=dq/dt。一般說來，上述感應電動勢與充放電電流將分布在電路的每一個微小段落上。然而，當交流電路的幾何線度與該交流電相應的電磁波波長相比很小時，則除開磁場較集中的電感線圈之外，電路其他段落上的感應電動勢都可忽略不計；另外除開電場較集中的電容器之外，電路其他段落上電荷的充集和放散也都可忽略不計。對這種電路可以用所謂集中參數來描述，即將電路中的電阻集中到有限個理想電阻元件上；磁場較集中的電感線圈以參數L=Ф/i來描述,稱為電感，構成理想電感元件；電場較集中的電容器以參數C＝q/u來描述,稱為電容,構成理想電容元件。這樣就構成了一個含有有限個理想元件的電路模型，這種電路稱為集中參數電路。例如對工頻50赫交流來說，在真空（或空氣）中的電磁波長有6000千米，所以通常遇到的工頻交流電路都是集中參數電路。
對集中參數電路來說，基爾霍夫電路定律在任何瞬間都成立。這是因為電路的分析並不涉及電感線圈內部或電容器內部，而只是把它們化作理想電感元件和理想電容元件去研究它們外部的電壓電流關係，在這些元件外部任何電路段落上不存在感應電動勢與充放電電流。因此，在任何瞬間，流入某節點的電流瞬時值的代數和恆等於零〔基爾霍夫電流定律(KCL)〕，即∑i＝0；沿任意閉合迴路各電壓瞬時值的代數和也恆等於零〔基爾霍夫電壓定律(KVL)〕，即∑u=0。
除基爾霍夫電路定律之外，各電路元件上的電壓和電流的約束關係也是分析電路問題所不可缺少的。在這三種元件上電壓瞬時值u與電流瞬時值i的關係是：
在電阻元件上：u=Ri, (2)
在電感元件上：u=dФ/dt=d(Li)/dt，(3)
在電容元件上：i=dq/dt=d(Cu)/dt，(4)
以上各式中R、L、C 就是各理想元件的參數:電阻、電感和電容。如果它們都是既不隨電壓、電流量值而改變的量（即線性的），又是不隨時間而改變的量（即非時變的），就被稱為線性非時變元件，其參數即線性非時變參數。
根據基爾霍夫兩條定律及各元件上的電壓、電流約束關係，就可以列出電路的微分方程。對交流電路來說，往往只須求出所謂穩定狀態（簡稱穩態）的解答，這相當於電路閉合後經過相當長的時間所建立的狀態。而電路經過開關切換從一個穩態過渡到另一個穩態之間的過程則稱為瞬變狀態(簡稱暫態)。暫態所經歷的時間理論上是無限長，但實際上往往只經過數秒、數毫秒、數微秒甚至更短的時間後即可認為已經結束，而已建立起新的穩態。暫態實際所經歷時間的長短決定於電路的參數。在暫態中各元件上電壓和電流一般都是非周期的，所以不在本條目討論的範圍之內。
下面將只討論由線性非時變元件所組成的集中參數交流電路。對這種電路來說，其微分方程是常係數線性微分方程組，它的穩態解就是方程的一組特解。
有效值和平均功率
交變電流的瞬時值i隨時間變動。工程上所用的交流電量值是通過該交流電流經電阻時所消耗的功率去衡量的。若某交流電流經一線性非時變電阻R在一個周期內消耗的能量與某直流I流經此同一電阻在同一時間內消耗的能量相等,則此直流I的量值就被定義為該交流i的有效值。據此，有下列等式關係
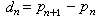(5)
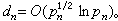(6)
對交變電壓或周期電壓，可用同樣方法來定義其有效值
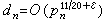。 (7)
(8)
a＝Amsin(ωt+═), (9)
它可以表示正弦電壓、正弦電流或其他任何正弦變數。式(9)中的 ω=2 πf為正弦變數的角頻率, A m為正弦變數的振幅或峰值。 ωt+═被稱為正弦變數在某一瞬時 t的相位,而═是 t=0（初始）時的相位,被稱為初相。因為相位常以角度表示，故又稱為相角。
當角頻率、振幅及初相都確定以後，正弦變數的瞬時值及其變動規律就已完全被確定，所以它們常被稱之為正弦變數的三要素。
正弦變數可以用複數表示，其模等於正弦變數的振幅,其幅角等於正弦變數的初相。例如有正弦電流 i= I msin( ωt+═)，則它的複數記作
式中j為虛數單位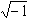 
。這個複數在複平面上（圖1）可看作一個矢量，其長度為 I m，由實軸起算的幅角即為 ═。如果讓這個矢量從圖示的初始位置 
以 ω為角速率逆時針方向鏇轉,則在任一時刻 t其幅角就將是該正弦電流在 t時刻的相位 ωt+═，而此時矢量在虛軸上的分量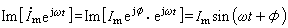 
也就是該正弦電流的瞬時值。但是這種矢量與空間矢量的意義全然不同,它在圖中的方向並不代表空間方向,而是代表著正弦變數的相位，故稱相量。用相量表示各正弦變數，從而分析或尋求各量之間關係的方法就是相量法。 
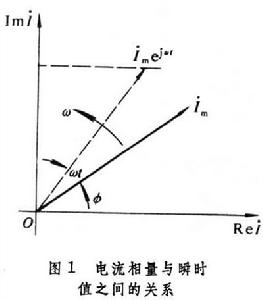交流電 在處理同頻率的正弦變數之間的關係時，由於代表它們的相量都是以相同的角速率在複平面上鏇轉，它們間的相對位置永遠不變，所以只須考慮它們的初始位置，如圖1中的相量
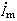而無須考慮其鏇轉速率。 正弦變數的有效值按方均根值計算可得
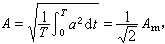(10)
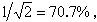這對正弦電壓、電流、磁通等都相同。 在工程上,表示交變電壓的大小都用有效值,故在計算正弦電流電路時就常用有效值相量來代替上述的振幅值相量。這兩種相量間成常數倍率的關係,即
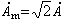。有效值相量 妅的模就是有效值 A。這樣，從有效值相量推求瞬時值的公式就是 
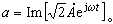(11)
用相量表示正弦變數的方便在於能將同頻率正弦量的相加減化為相量（即複數）的相加減，把正弦量對時間的求導和積分化為與j ω的相乘除從而可簡化計算；同時還可以把相互有關係的相量畫在同一個複平面中，以表示它們所代表的各個正弦變數的相對量值大小和相位關係，這種圖形被稱為相量圖。
於是，基爾霍夫兩條定律就可以從描述瞬時值的代數和恆等於零化為各該相量的代數和為零，即對任一節點有
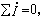而對任一迴路則有 
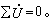這些關係常被稱為基爾霍夫定律的相量形式。 下面再尋求交流電路中常見的三種元件電阻、電感和電容上電壓電流間的相量關係,即將式(2)、(3)、(4)化為相量形式。
當正弦變數乘以常量時，其振幅將成比例地增長而相位則不變，故表示其積的相量也等於原相量乘以常量。因此在電阻元件上電壓電流的相量關係根據式 (2)應為
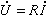，它表示電阻上電壓電流有效值的比仍是電阻 R，且電壓與電流同相位。 當尋求相量對時間的導數時，必須先補入 鏇轉因子
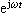再進行求導，然後約去 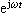。這樣，相量對時間求導就化為該相量乘以j ω。據此，在電感元件上電壓電流的相量關係根據式(3)化為 
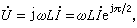它表示電感元件上電壓有效值等於電流有效值乘以 ωL，而電壓在相位上則超前於電流90°。同樣,從式(4)可知,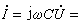 
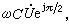它表示電容元件上電壓有效值等於電流有效值乘以 1/ ωC，而電壓在相位上則滯後於電流90°。 對時間的積分是求導的反運算，因此相量對時間求積分應化為該相量除以j ω。
阻抗與導納 由線性非時變元件構成的電路通入某一頻率的正弦電流時，電路的電壓也必然是同一頻率的正弦電壓。這時電壓相量與電流相量的比
(12)
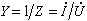(13)
阻抗和導納都可以寫成指數形式，也都可以寫成代數形式： Z=| Z|e jθ = R+j X； Y=| Y|e
= G+j B，它們的模| Z|及| Y|分別稱為阻抗模及導納模，等於電壓與電流兩有效值的比。幅角 θ稱為 阻抗角,代表電壓在相位上超前於電流的角度。代數式中的各參數： R＝| Z|cos θ稱為電路的電阻； X=| Z|sin θ稱為電路的電抗； G＝ Ycos θ稱為電路的電導； B=- Ysin θ則稱為電路的電納。這些參數之間的關係可以用兩個相似的直角三角形來表示，如圖2a及b,它們分別稱為 阻抗三角形和導納三角形。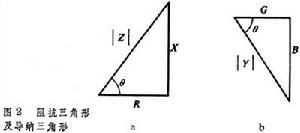 
交流電 阻抗和導納的概念，只能適用於頻率一定的正弦電壓或電流。如果頻率變動，阻抗和導納一般也都要隨著變動。因此一般說來，阻抗、導納、電阻、電抗、電導、電納以及阻抗角都是頻率或角頻率的函式。
採用相量表示正弦電流電路，把電壓與電流用它們的相量表示，就得到與直流電路完全相似的 歐姆定律和 基爾霍夫電路定律。直流電路中的電阻與電導則分別被阻抗與導納所取代。因此，套用相量法計算正弦電流電路時就可以用直流電路計算的各種定理和方法。例如，當若干阻抗 Z 1、 Z 2、……相串聯時，其等效阻抗 Z等於各阻抗之和: Z= Z 1+ Z 2+……；而若干導納 Y 1、 Y 2、……相併聯時,其等效導納 Y也等於各導納的和： Y＝ Y 1+ Y 2+……。
根據上面所討論電阻、電感和電容元件上的電壓電流相量關係,可知電阻元件的阻抗為實量 R；電感元件的阻抗為j ωL,是虛量,其量值 X L= ωL 稱為感抗；電容元件的導納為j ωC，或其阻抗為-j/( ωC),也是虛量，其量值 X c＝1/( ωC)稱為容抗。感抗和容抗的倒量 B L=1/( ωL)及 B c＝ ωC 則分別稱為感納及容納。
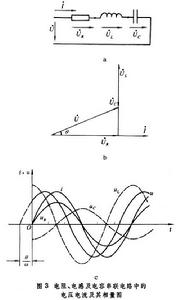
如果電路由電阻 R、電感 L及電容 C串聯組成(圖3a)，則其阻抗應等於三個元件阻抗的和,即
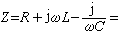
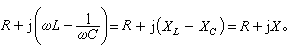若已知電壓 妧，則電流 夒可根據歐姆定律求得
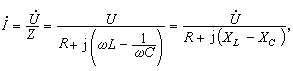
交流電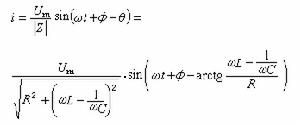 
圖3c繪出了電流i、電壓 u及各元件上電壓分量uc、uL、uc隨時間變動的曲線。
正弦電流的功率
當線性非時變參數電路中通過正弦電流i時，電路上的電壓為同一頻率的正弦電壓u。如果電流和電壓的初相各為═i及═u,則按式(8)求得此電路消耗的平均功率為
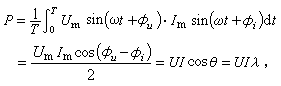(14)
在一般情況下，平均功率的計算式與直流電路中的不同，並不等於電壓電流兩有效值的相乘積，而是要在此乘積上乘上一個小於1的數 λ＝cos θ。它稱為功率因數。電壓電流兩有效值的乘積 S= UI則稱為視在功率或表觀功率。為了與平均功率相區別，視在功率習慣上常用伏安(V·A)作單位，而不用瓦。
當用相量表示電壓、電流時，把這兩個相量直接相乘是沒有意義的。但若取電流相量的共軛
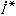與電壓相量妧相乘，則得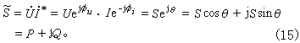 
它稱為復功率，其實部Scosθ就是平均功率P，也可稱為有功功率；虛部Ssinθ則稱為電路的無功功率Q。無功功率並不反映電路吸收的功率，只是反映電路與外電源之間能量反覆授受的程度，其單位常稱為無功伏安或乏。
一般電氣設備都有電壓的額定值和電流的額定值，其容量以視在功率標出。如果這種設備運行時功率因數不是固定的,例如交流同步發電機或變壓器都是這樣,其功率因數與負載性質有關。為了充分利用這類電氣設備的容量，就應該儘可能提高功率因數，也就是應設法使各種負載的無功功率能互相補償〔按式(15)，無功功率可為正值(當θ＞0)或負值(當θ＜0)〕,或者儘可能提高每一負載的功率因數。另外當功率因數小於1時,總有一部分能量在電源和負載之間反覆授受，致使傳輸線上因電流增大而效率降低。這也是要儘量提高功率因數的一條理由。
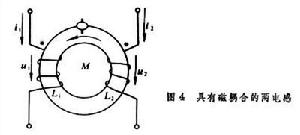
交流電路中的互感
當交流電路中各部分之間存在著磁耦合時，則還須考慮互感。它可以看作是電阻、自感（當不存在互感時，自感可徑稱為電感）、電容之外的另一參數。設兩個理想的線性非時變電感元件其各自的自感為L1及L2,其間的互感為M(圖4)，則兩元件上的電壓、電流瞬時值關係是
(16)
(17)
交流電 通常一個元件上電壓和電流的參考方向（即正值所表示的實際方向）都是規定為相一致的。但一個元件中電流的參考方向與另一個元件中電流的參考方向之間在無互感的情況下，規定時並無任何約束。然而在有互感的情況下,為了使互感 M得出正值,還必須要求兩元件中電流同為正值（或同為負值）時其磁場應相互加強，如圖4所示。由於簡化電路圖中並不畫出電感線圈的繞法,所以常用星號“ * ”標示磁耦合的對應端。當兩線圈中電流的實際方向都是從對應端進入（或離開）線圈時,其磁場就是相互加強。圖4中已作了對應端標記。
當兩電感元件中電壓、電流都是同一頻率的正弦變數時，式(16)、(17)可以寫成相量形式
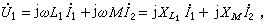(18)
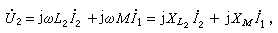(19)
用這兩式來共同表達兩個元件上電壓電流相量的約束關係。這裡XM＝ωM 稱為兩元件間的互感電抗。
具有磁耦合的兩個電感元件也可以當作一個整體而看成一個具有四個端子的元件。
非正弦周期交流電路
前面曾提到：正弦變數是周期變數中最簡單和最基本的形式，這是因為根據數學中的傅立葉方法，周期變數常可以分解成一系列正弦變數的和〔作這種分解的條件是f（t）必須滿足所謂狄利克雷條件，但一般電路中遇到的周期變數都能滿足這個條件〕，即
(20)
其中各係數 A0，A1…及各初相═1，═2…都可根據特定的公式算出。當f(t)代表電流時,A0就相當於該電流的直流成分。式中的每一個正弦項Aksin(kωt+═k)稱為一個諧波。當k=1時稱為基波,k為大於1的整數時則稱為高次諧波或k次諧波。一般隨諧波次數k的增高其振幅Ak也會逐漸變小，所以式(20)右端可視所需精度取到一定的諧波次數為止。
一般的交流電源，其電壓常與正弦電壓有某些差別，亦即存在一些高次諧波。當線性非時變參數交流電路中各電源電壓都是同一周期的周期變數時，則建立穩態後各電流以及負載上的電壓一般也都是具有相同周期的周期變數。欲計算此種電路的電壓電流時，可根據線性電路的疊加定理，先將給定的電壓電流分解為諧波，然後分別對每一諧波進行計算（可用相量法），並將各個相對應的計算結果寫成瞬時值，然後相加即可。
電力傳輸
交流電被廣泛運用於電力的傳輸，因為在以往的技術條件下交流輸電比直流輸電更有效率。傳輸的電流在導線上的耗散功率可用P＝I^2×R（功率＝電流的平方×電阻）求得，顯然要降低能量損耗需要降低傳輸的電流或電線的電阻。由於成本和技術所限，很難降低目前使用的輸電線路（如銅線）的電阻，所以降低傳輸的電流是唯一而且有效的方法。根據P=IV（功率＝電流×電壓，實際上P=IVcosφ），提高電網的電壓即可降低導線中的電流，以達到節約能源的目的。
而交流電升降壓容易的特點正好適合實現高壓輸電。使用結構簡單的升壓變壓器即可將交流電升至幾千至幾十萬伏特，從而使電線上的電力損失極少。在城市內一般使用降壓變壓器將電壓降至幾萬至幾千伏以保證安全，在進戶之前再次降低至市電電壓(大陸、香港220V）或者適用的電壓供用電器使用。一般使用的交流電為三相交流電，其電纜有三條火線和一條公共地線，三條火線上的正弦波各有120°之相差。對於一般用戶只使用其中的一或兩條相線（一條時需要地線）。
近年來直流變壓及輸電技術取得了長足的發展，而高壓直流輸電的浪費會比較小；因此未來有望取代交流電以解決交流電的安全性和交直流轉換問題。
交流電正弦波【交流電的頻率和周期】頻率是表示交流電隨時間變化快慢的物理量。即交流電每秒鐘變化的次數叫頻率，用符號f表示。它的單位為周／秒，也稱赫茲常用“Hz”表示，簡稱周或赫。例如市電是60周的交流電，其頻率即為f=60周／秒。對較高的頻率還可用千周（kC）和兆周（MC）作為頻率的單位。
1千周（kC）=103周／秒
1兆周（MC）=10千周（kC）=106周／秒
例如，中國第一顆人造地球衛星發出的訊號頻率是20.009兆周，亦即它發出的是每秒鐘變化20.009×106次的交變訊號。交流電正弦電流的表示式中I=Imsin（ωt+φ0）中的ω稱為角頻率，它也是反映交流電隨時間變化的快慢的物理量。角頻率和頻率的關係為
ω=2πf。
交流電隨時間變化的快慢還可以用周期這個物理量來描述。交流電變化一次所需要的時間叫周期，用符號T表示。周期的單位是秒。顯然，周期和頻率互為例數，即
由此可見，交流電隨時間變化越快，其頻率f越高，周期T越短；反之，頻率f越低，周期T越長。
峰值
交流電 i=Imsin（εt＋α）
中的Im叫做電流的峰值，i為瞬時值。應該指出，峰值和位相是按上式中Im為正值的要求定義的。如對下面形式的 函式
i=-5sin（ωt+α）
不應認為峰值為-5、初相為+α，而應把函式先寫成
i=5sin（ωt+α+π）
從而看出其峰值為5，初位相為α＋π。
效值
交流電 dW=i2Rdt
在一個周期內交流電在電阻上產生的總熱量
而直流電I在同一時間T內在該電阻上產生的熱量
W=I2RT
根據有效值的定義有
所以有效值
根據上式，有時也把有效值稱為“平均根值”。對正弦交流電，有i=Imsinωt，故
而其中
可見正弦交流電的有效值等於峰值的0.707倍。通常，交流電錶都是按有效值來刻度的。一般不作特別說明時，交流電的大小均是指有效值。例如市電220伏特，就是指其有效值為220伏特，
平均值
交流電 對正弦交流電流，即i=Imsinωt，則平均值與峰值的關係為
故，正弦交流電的平均值等於峰值的0.637倍。對正弦交流電來說在上半周期內，一定量的電量以某一方向流經導體的橫截面，在下半周期內，同樣的電量卻以相反的方向流經導體的橫截面。因而在一個周期內，流經導體橫截面的總電量等於零，所以在一個周期內正弦交流電的電流平均值等於零。如果直接用磁電式電錶來測量交流電流，將發現電錶指針並不發生偏轉。這是因為交流電流一會兒正，一會兒為負，磁電式電錶的指針無法適應。如果附有整流器的磁電式電錶（例如萬用電錶中的交流檔）接入交流電路中如圖3－46所示。那么在一周期內，只有正半周的電流通過電錶，如圖3－47中的實線所示，負半周期電流則過二極體D2而不通過表，圖3－47中的虛線所示。在一周期內通過電錶的電流平均值為
即半波整流後交流電的平均值和最大值的關係為
而交流電的有效值和最大值的關係為
所以
即正弦交流電經半波整流後的平均值只有有效值的0.45倍。
位相
交流電 電阻
純電阻電路是最簡單的一種交流電路。白熾燈、電爐、電烙鐵等的電路都可以看成是純電阻電路。雖然純電阻的電壓和電流都隨時間而變，但對同一時刻，歐姆定律仍然成立，即的波形如圖3－49b所示。對純電阻電路有：（1）通過電阻R的電流和電壓的頻率相同；（2）通過電阻R的電流峰值和電壓峰值的關係是的電流和電壓同位相。
相關詞條
參考資料
1、李瀚蓀編：《電路分析基礎》，第二版，下冊，人民教育出版社，北京，1983。
2、江澤佳主編：《電路原理》，第二版，上冊，人民教育出版社，北京，1985。
3、C.A.狄蘇爾、葛守仁著，林爭輝主譯：《電路基本理論》,上冊,人民教育出版社,北京,1979。(C.A. Desoerand E.S.Kuh,Basic Circuit Theory，McGraw-Hill,New York,1969.)
4.http://www.pw0.cn/article/xinwen
5.http://zhidao.baidu.com/question/70447425.html?quesup1
關於電資源的相關知識
| 節約用電對發展國民經濟有重要意義。電能是由一次能源（煤、石油、天然氣、水利資源等）轉換而成的二次能源。耗電量的減少可以使發電、輸變電所需要的設備容量減少，節約能源方面的投資。 |
電工學知識
| 伴隨新技術革命和教學改革的不斷深入，當前套用電工學迅速發展，由於電工學的套用領域不斷擴大，電工學的知識也必不可少。 |
