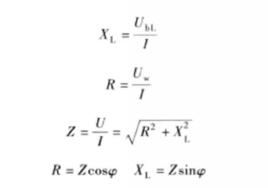基本介紹
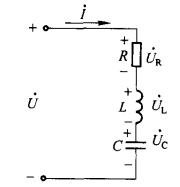 圖1RLC 串聯電路
圖1RLC 串聯電路電阻、電感和電容串聯的電路如圖1所示。
 阻抗三角形
阻抗三角形串聯後對電流的阻礙作用稱為阻抗,用字母Z表示,單位為歐姆(n)。阻抗的複數表達式為
 阻抗三角形
阻抗三角形 阻抗三角形
阻抗三角形式中,X稱為電抗,單位為歐姆( )。
 阻抗三角形
阻抗三角形阻抗值為
 阻抗三角形
阻抗三角形 阻抗三角形
阻抗三角形 阻抗三角形
阻抗三角形式中, 三者之間符合直角三角形的關係,如圖2所示,稱其為 阻抗三角形。三角形中的 稱為阻抗角
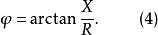 阻抗三角形
阻抗三角形 圖2 阻抗三角形
圖2 阻抗三角形 阻抗三角形
阻抗三角形由式(4)表明:當電流的頻率一定時,電路的性質(電壓與電流的相位差 )由電路的參數R、L、C決定。
 阻抗三角形
阻抗三角形 阻抗三角形
阻抗三角形 阻抗三角形
阻抗三角形 阻抗三角形
阻抗三角形 阻抗三角形
阻抗三角形(1)當X>0時,即 時,此時 ,表明電壓超前電流 角,如表1(a)所示。電感電壓 補償電容電壓 後尚有餘量,即電感的作用大於電容的作用,此時電路呈 電感性。
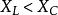 阻抗三角形
阻抗三角形 阻抗三角形
阻抗三角形 阻抗三角形
阻抗三角形 阻抗三角形
阻抗三角形 阻抗三角形
阻抗三角形(2)當X<0時,即 時,此時 ,表明電壓滯後電流 角。電容電壓 補償電感電壓 後尚有餘量,即電容的作用大於電感的作用,此時電路呈 電容性。
 阻抗三角形
阻抗三角形 阻抗三角形
阻抗三角形(3)當X=0時,即 時,此時 ,表明電壓與電流同相,此時電路呈電阻性 。
電壓三角形
 阻抗三角形
阻抗三角形 阻抗三角形
阻抗三角形根據KVL定律,利用阻抗三角形,就可得出 串聯電路的各個電壓之間的關係。在表1中, 串聯,三者流過的電流相同,設電流為
 阻抗三角形
阻抗三角形根據KVL定律可得
 阻抗三角形
阻抗三角形對應的電流電壓有效值相量表達式為
 阻抗三角形
阻抗三角形 阻抗三角形
阻抗三角形 阻抗三角形
阻抗三角形由式(4)可見,將阻抗三角形的各個邊乘以電流 就可得到 串聯的電壓關係圖,如圖3所示 。
 (a)電壓相量圖 (a)電壓相量圖 | 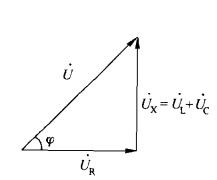 (b)相量三角形 (b)相量三角形 | 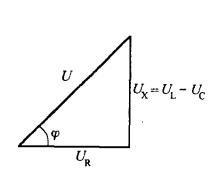 (c) 電壓三角形 (c) 電壓三角形 |
 阻抗三角形
阻抗三角形 阻抗三角形
阻抗三角形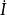 阻抗三角形
阻抗三角形表1(a)為電壓相量圖, 為電壓 與電流 之間的相位差,數值上與阻抗角相等。表1(b)為電壓相量三角形,表1(c)是電壓有效值三角形,簡稱電壓三角形,有效值之間的關係為
 阻抗三角形
阻抗三角形電壓與電流有效值之間的關係為
 阻抗三角形
阻抗三角形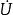 阻抗三角形
阻抗三角形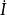 阻抗三角形
阻抗三角形與 之間的相位差為
 阻抗三角形
阻抗三角形功率三角形
 圖3
圖3 阻抗三角形
阻抗三角形將電壓三角形的各個邊乘以電流 ,就可得到功率三角形,如圖3所示。
圖3中P為有功功率,即電阻所消耗的功率,單位是瓦[特](W),則
 阻抗三角形
阻抗三角形圖3中Q為總的無功功率,是L和C串聯後與電源之間的互換功率,單位是乏(var),則
 阻抗三角形
阻抗三角形上式說明L和C兩種儲能元件同時接在電路中,兩者之間可進行存儲能量之間的互換,減少了與電源之間能量的互換。
圖3中S稱為視在功率,是電源所提供的功率,單位為伏安(V·A),則
 阻抗三角形
阻抗三角形 阻抗三角形
阻抗三角形圖3中的 稱為功率因數角,在數值上功率因數角、阻抗角和總電壓與電流之間的相位差,三者之間是相等的。
 阻抗三角形
阻抗三角形阻抗三角形、電壓三角形和功率三角形是分析計算 串聯或其中兩種元件串聯的重要依據 。