算法
 二分法查找
二分法查找1.開始令front=0(指向3),end=7(指向88),則mid=3(指向36)。因為mid>x,故應在前半段中查找。
2.令新的end=mid-1=2,而front=0不變,則新的mid=1。此時x>mid,故確定應在後半段中查找。
3.令新的front=mid+1=2,而end=2不變,則新的mid=2,此時a[mid]=x,查找成功。
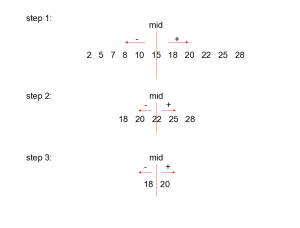
如果要查找的數不是數列中的數,例如x=25,當第三次判斷時,x>a[mid],按以上規律,令front=mid+1,即front=3,出現front>end的情況,表示查找不成功。
例:在有序的有N個元素的數組中查找用戶輸進去的數據x。
算法如下:
1.確定查找範圍front=0,end=N-1,計算中項mid(front+end)/2。
2.若a[mid]=x或front>=end,則結束查找;否則,向下繼續。
3.若a[mid]<x,說明待查找的元素值只可能在比中項元素大的範圍內,則把mid+1的值賦給front,並重新計算mid,轉去執行步驟2;若a[mid]>x,說明待查找的元素值只可能在比中項元素小的範圍內,則把mid-1的值賦給end,並重新計算mid,轉去執行步驟2。
[一維數組,折半查找]
複雜度分析
時間複雜度
1.最壞情況查找最後一個元素(或者第一個元素)Master定理T(n)=T(n/2)+O(1)所以T(n)=O(logn)
2.最好情況查找中間元素O(1)查找的元素即為中間元素(奇數長度數列的正中間,偶數長度數列的中間靠左的元素)
空間複雜度
S(n)=n
C代碼
 二分法查找
二分法查找{
int mid;
if(low > high)
return -1;
mid = (low + high)/2;
if(a[mid] == key) return mid;
else if(a[mid] > key)return search(a,key,low,mid -1);
else return search(a,key,mid + 1,high);
}
int main()
{
int a[] = {1,2,3,4,5,6,7,8,9,12,13,45,67,89,99,101,111,123,134,565,677};
int i = search(a,99,0,sizeof(a)/sizeof(a[0])-1);
cout << i <<endl;
return 0;
}
C++代碼
#include<iostream>
#define N 10
using namespace std;
int main()
{
int a[N],front,end,mid,x,i;
cout<<"請輸入已排好序的a數組元素:"<<endl;
for(i=0;i<N;i++)
cin>>a[i];
cout<<"請輸入待查找的數x:"<<endl;
cin>>x;
front=0;
end=N-1;
mid=(front+end)/2;
while(front<end&&a[mid]!=x)
{
if(a[mid]<x)front=mid+1;
if(a[mid]>x)end=mid-1;
mid=(front+end)/2;
}
if(a[mid]!=x)
cout<<"沒找到!"<<endl;
else
cout<<"找到了!在第"<<mid+1<<"項里。"<<endl;
return 0;
}
pascal代碼
function found(a,b,c:longint):longint;
var d,e:longint;
begin
d:=(a+b) div 2;
if m[d]=c then found:=d{找到了數字所在位置}
else if m[d]<c then if (d+1)>b then found:=0{表明不在數列之中}
else found:=found(d+1,b,c){查找比m[d]大的數}
else if (d-1)<a then found:=0
else found:=found(a,d-1,c){查找比m[d]小的數};
end;

