基礎知識
自然界中的有兩類現象,確定性現象和隨機現象。
確定性現象:在一定的條件下必然發生(或不發生)某種結果的現象。
例如:太陽從東方升起;水在標準大氣壓下加溫到100℃沸騰。
隨機現象:在基本條件不變的條件下,一系列試驗(或觀察)常會得到不同的結果。
例如:擲一枚硬幣,正面朝上或反面朝上;一天內進入某超市的顧客數。
隨機現象的統計規律性: 隨機現象的各種結果會表現出一定的規律性,這種規律性稱之為統計規律性。
隨機事件的特徵是具有現象的不確定性,但是我們可以通過重複觀測,從不確定現象中尋找、觀察特定事件發生的規律,為此需要讓某一隨機現象重複發生(不一定是人為控制的)並記錄觀測結果,稱之為隨機試驗
隨機試驗的三個特徵:①可以在相同條件下重複進行;②事先知道可能出現的結果;③進行試驗前並不知道哪個試驗結果會發生。
樣本點:隨機試驗的每一個可能結果。
樣本空間:雖然隨機事件的結果是不確定的,但結果的範圍必須是已知的,可以描述的。把隨機試驗的每一種可能出現的(不能再分割的)結果稱為隨即試驗的樣本點或者基本事件,所有可能結果的集合,也就是樣本點的總和稱為隨機試驗的樣本空間。樣本空間分為三類:離散樣本空間、連續樣本空間、混合型 。
定義
事件域的元素應該包括樣本空間和空集;其次應該保證事件經過並、交、差、對立各種運算後仍然是事件,即其對集合的運算有封閉性。(交的運算可以通過並與對立來實現;差的運算可通過對立與交來實現)。
設Ω為樣本空間,F 是由Ω的子集組成的集合類,若F滿足以下三點:
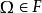 事件域
事件域 事件域
事件域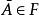 事件域
事件域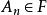 事件域
事件域 事件域
事件域1. ;2.若 ,則 ;3.若 ,n=1,2...,則 。
 事件域
事件域 事件域
事件域則稱 F 為波雷爾 ( Borel事件域),或 事件域或 代數。波雷爾事件域中每一個樣本空間的子集稱為一個事件。( Ω,F )為可測空間 。
基本類型
1.樣本空間包含可列(可數)的元素,從而事件域包含可列個事件,生成的機率是離散型機率;
2.樣本空間包含不可數的元素,從而事件域包含不可數的事件,生成的機率是連續型機率 。
相關內容
樣本空間Ω與事件域F是抽象的、理論上是存在的;
事件域 F是集類,隨機事件是集合且是 F中的元素;
事件必是樣本空間的子集,但樣本空間的子集並非是事件;
必然事件與不可能事件也稱為隨機事件;
事件發生是指若且唯若出現了該事件所含的某一基本事件 。
1.樣本空間Ω與事件域F是抽象的、理論上是存在的;
2.事件域 F是集類,隨機事件是集合且是 F中的元素;
3.事件必是樣本空間的子集,但樣本空間的子集並非是事件;
4.必然事件與不可能事件也稱為隨機事件;
5.事件發生是指若且唯若出現了該事件所含的某一基本事件 。
例子分析
例1.擲一枚硬幣。
分析:出現“正面”、“反面”都是基本事件。這兩個基本事件構成一個樣本空間。在例1中共有兩個樣本點:“正面”,“反面”。作F={正面或反面,正面,反面,空集},它構成一個波雷爾事件域,其中每一個元素都是一個事件。需要說明,F表達式中的花括弧。是指事件的集合。
例2.擲一顆骰子。
 事件域
事件域 事件域
事件域 事件域
事件域 事件域
事件域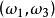 事件域
事件域 事件域
事件域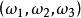 事件域
事件域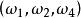 事件域
事件域 事件域
事件域 事件域
事件域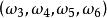 事件域
事件域 事件域
事件域 事件域
事件域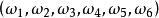 事件域
事件域分析:出現“1點”、“2點”、“3點”、“4點”、“5點”、“6點”都是基本事件。這六個基本事件構成一個樣本空間。在例2中共有六個樣本點,記 為出現“i點”的樣本點,i=1,2,3,4,5,6。作F={ ... ,( ), ... , , ... , ... , ... , 它構成一個波雷爾事件域。這裡每一對小括弧表示它所包含的樣本點的集合。

