不動點算法
正文
又稱固定點算法。所謂不動點，是指將一個給定的區域A,經某種變換ƒ(x),映射到A時,使得x=ƒ(x)成立的那種點。最早出現的不動點理論是布勞威爾定理(1912)：設A為Rn中的一緊緻凸集, ƒ為將A映射到A的一連續函式，則在A中至少存在一點x，使得x=ƒ（x）。其後，角谷靜夫於1941年將此定理推廣到點到集映射上去。設對每一x∈A ，ƒ(x)為A的一子集。若ƒ(x)具有性質：對A上的任一收斂序列xi→x0，若 yi∈ƒ(xi)且yi→y0，則有y0∈ƒ(x0),如此的ƒ(x)稱為在A上半連續，角谷靜夫定理：設A為Rn中的一緊緻凸集，對於任何x∈A，若ƒ(x)為A的一非空凸集，且ƒ(x)在A上為上半連續，則必存在x
∈A,使x∈ƒ(x)。J.P.紹德爾和J.勒雷又將布勞威爾定理推廣到巴拿赫空間。 不動點定理在代數方程、微分方程、積分方程、數理經濟學等學科中皆有廣泛的套用。例如，關於代數方程的基本定理，要證明ƒ(x)=0必有一根，只須證明在適當大的圓│x│≤R 內函式ƒ(x)+x有一不動點即可；在運籌學中，不動點定理的用途至少有二：一為對策論中用來證明非合作對策的平衡點的存在和求出平衡點；一為數學規劃中用來尋求數學規劃的最優解。對於一個給定的凸規劃問題：min{ƒ(x)│gi(x)≤0，i=1,2,…,m}，在此,ƒ和g1,g2,…,gm皆為Rn中的凸函式。通過適當定義一個函式φ,可以證明：若上述問題的可行區域非空，則φ的不動點即為該問題的解。
在1964年以前，所有不動點定理的證明都是存在性的證明，即只證明有此種點存在。1964年，C.E.萊姆基和 J.T.Jr.豪森對雙矩陣對策的平衡點提出了一個構造性證明。1967年，H.斯卡夫將此證法套用到數學規劃中去。其後，不動點定理的構造性證明有了大的發展和改進。
H.斯卡夫的證明是基於一種所謂本原集，後來的各種發展皆基於某種意義下的三角剖分。現以n 維單純形Sn為例來說明這一概念，在此,
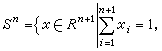
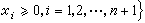。對每一i, 將區間0≤xi≤1依次分為m1,m2…等分，m1<m2<…,mi→
,是給定的一列正整數。對於固定的i,過分點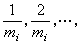
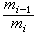依次作平行於xi=0的平面。 這些平面將Sn分成若干同樣大小的n維三角形。它們的全體作成的集 Gi,稱為Sn的一三角剖分。設ƒ(x)為 Sn→Sn的一連續函式，x＝(x1,x2,…,xn+1),ƒ（x）=（ƒ1（x），ƒ2（x），…，ƒn+1（x））。定義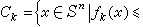
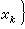。由於ƒ(x)和x皆在Sn上,若有
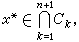則顯然有ƒ(x)=x,即x為ƒ(x)的一不動點。 對每一點y∈Sn賦與標號l(y)=k=min{j│y∈Cj,且yj>0}。由著名的施佩納引理,在Gi中必存在一三角形σi，它的n+1個頂點yi(k)的標號分別為k(k=1,2,…,n+1)於是可得一列正數ij(j→
),使得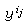
(k)→yk,k=1,2,…,n+1。根據σi的作法，當ij→時,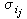
收斂成一個點x。故yk=x,k=1,2,…,n+1。因 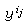(k)的標號為k,故yk∈Ck,因而
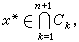即x為所求的不動點。因此,求ƒ(x):Sn→Sn 的不動點問題就化為求 σi(i=1,2,…) 的問題。為了計算上的效果，除了上述的標號法之外，還有標準整數標號法、向量標號法等等。關於如何求σi，有變維算法、三明治法、同倫算法、變維重始法等等，通過適當定義,可將上之Sn改為Rn或Rn中之一凸集。求一凸函式在一凸集上的極值問題也可化為求不動點問題。一般說來，這條途徑適用於維數不高但問題中出現的函式較為複雜的情況。 參考書目
A.J.J.TalmanVariable Dimension Fixed Point Algorithms and Triangulations, Mathematisch Centrum, Amsterdam, 1980.
