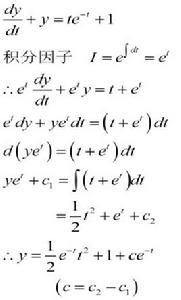定義
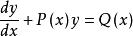一階線性微分方程
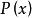一階線性微分方程
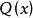一階線性微分方程形如（記為式1）的方程稱為一階線性微分方程。其特點是它關於未知函式y及其一階導數是一次方程。這裡假設，是x的連續函式。
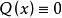一階線性微分方程
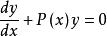一階線性微分方程若，式1變為 （記為式2）稱為 一階齊線性方程。
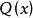一階線性微分方程如果不恆為0，式1稱為 一階非齊線性方程，式2也稱為對應於式1的 齊線性方程。
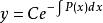一階線性微分方程式2是 變數分離方程，它的通解為，這裡C是任意常數。
通解求法
一階線性微分方程的求解一般採用常數變易法，通過常數變易法，可求出一階線性微分方程的通解。
一階齊次線性微分方程
對於一階齊次線性微分方程：
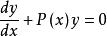一階線性微分方程其通解形式為：
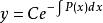一階線性微分方程其中C為常數，由函式的初始條件決定。
一階非齊次線性微分方程
對於一階非齊次線性微分方程：
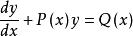一階線性微分方程 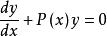一階線性微分方程其對應齊次方程: 解為：
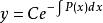一階線性微分方程令C=u(x)，得:
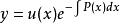一階線性微分方程
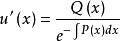一階線性微分方程帶入原方程得：
對u’(x)積分得u(x)並帶入得其通解形式為：
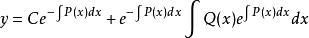一階線性微分方程其中C為常數，由函式的初始條件決定。
注意到，上式右端第一項是對應的齊線性方程式（式2）的通解，第二項是非齊線性方程式（式1）的一個特解。由此可知，一階非齊線性方程的通解等於對應的齊線性方程的通解與非齊線性方程的一個特解之和。
