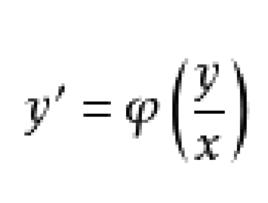齊次一階微分方程

形如y'=f(y/x)的一階微分方程，稱為齊次一階微分方程。齊次微分方程是一個微分方程，如果它的一個解乘以任意常數後，仍是它的解，則稱為齊次微分方程。對一階線性微分方程來說，右端(即不含未知函式及其導數的項)不為零的方程y′+p(x)y= q(x)稱為非齊次方程；與此對應的，右端q(x=0的方程y′+p(x)y=0，稱為對應的齊次方程。此外，當微分方程的左端是以自變數，未知函式作為變元的齊次函式時，也稱為齊次方程。

基本介紹

齊次一階微分方程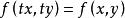

齊次一階微分方程

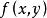齊次一階微分方程

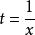齊次一階微分方程

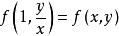齊次一階微分方程

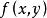齊次一階微分方程

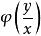齊次一階微分方程

如果對任何都有，則稱是x和y的 齊次函式，如果取，則。這就是說齊次函式可改寫為的形式。

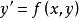齊次一階微分方程

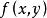齊次一階微分方程

一階微分方程(其中，為齊次函式)就叫做 齊次(一階微分)方程。或者說，方程

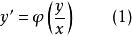齊次一階微分方程

是齊次方程。此外，如果在微分方程的每一項中，因子x和y的冪次的總和都是相等的，則該方程就是 齊次方程。

例如

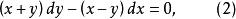齊次一階微分方程

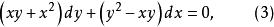齊次一階微分方程

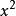齊次一階微分方程

都是齊次方程。事實上，式(2)各項同除x，式(3)各項同除以，則式(2)和(3)可分別化為

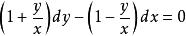齊次一階微分方程

或

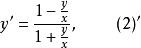齊次一階微分方程

和

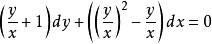齊次一階微分方程

或

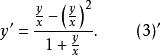齊次一階微分方程

另外，方程

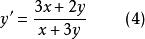齊次一階微分方程

也是齊次方程。事實上，方程(4)右端分子和分母同除以x，則得到齊次方程

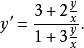齊次一階微分方程

一般解法

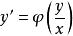齊次一階微分方程

關於齊次方程的一般解法如下 ：

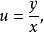齊次一階微分方程

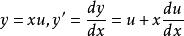齊次一階微分方程

令所以，代入方程(1)，得

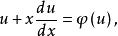齊次一階微分方程

即有

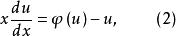齊次一階微分方程

方程(2)為可分離變數方程，於是

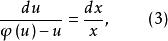齊次一階微分方程

方程(3)兩端積分，得

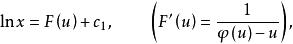齊次一階微分方程

上述等式可改寫為

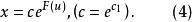齊次一階微分方程

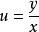齊次一階微分方程

把代入式(4)，則得到方程(1)的隱式通解

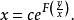齊次一階微分方程

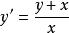齊次一階微分方程

例1求方程的通解。

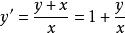齊次一階微分方程

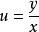齊次一階微分方程

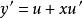齊次一階微分方程

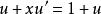齊次一階微分方程

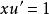齊次一階微分方程

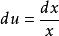齊次一階微分方程

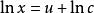齊次一階微分方程

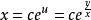齊次一階微分方程

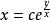齊次一階微分方程

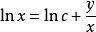齊次一階微分方程

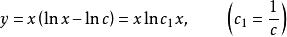齊次一階微分方程

解：方程，令，所以，於是方程變為，即，所以。積分得通解，即。也可以把方程的隱式通解改寫為顯式通解。事實上，因為，所以。