一階線性微分方程可分兩類，一類是齊次形式的，它可以表示為y'+p(x)y=0，另一類就是非齊次形式的，它可以表示為y'+p(x)y=Q(x)。
齊次線性方程與非齊次方程比較一下對理解齊次與非齊次微分方程是有利的。對於非齊次微分方程的解來講，類似於線性方程解的結構結論還是成立的。就是：非齊次微分方程的通解可以表示為齊次微分方程的通解加上一個非齊次方程的特解。
一階非齊次線性微分方程的求解：
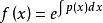非齊次線性微分方程
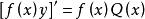非齊次線性微分方程1 一階非齊次線性微分方程y'+p(x)y=Q(x)，若設 ，則該方程的等價方程為 。
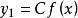非齊次線性微分方程2若 是一階齊次線性方程y'+p(x)y=0的通解，則一階非齊次線性方程y'+p(x)y=Q(x)的通解
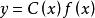非齊次線性微分方程
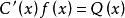非齊次線性微分方程解滿足。
二階非齊次線性微分方程的求解：
二階常係數非齊次線性微分方程的表達式為y''+py'+qy=f(x)，它的特解
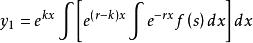非齊次線性微分方程
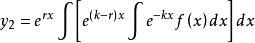非齊次線性微分方程，
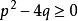非齊次線性微分方程（1） 當時，r和k都是實數，y*=y1是方程的特解。
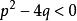非齊次線性微分方程（2）當時，r=a+ib,k=a-ib(b≠0)是一對共軛復根，y*=1/2（y1+y2）是方程的實函式解。
三階非齊次線性微分方程的求解：
三階常係數非齊次線性微分方程的表達式為y'''+p1y''+p2y'+p3y=f(x)，設其特徵方程的三個特徵跟分別是r1，r2，r3，特解為
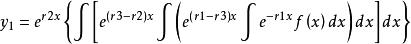非齊次線性微分方程
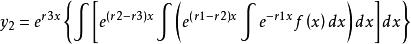非齊次線性微分方程（1）當r1，r2，r3都是實數時，y*=y1是方程的特解。
（2）當r1是實數，r2，r3是共軛複數時，則y1和y2是共軛複數，因此，y*=1/2（y1+y2）是方程的實函式解 。
高階非齊次線性微分方程的求解：
一般形式的n 階非齊次線性微分方程
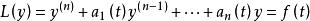非齊次線性微分方程對應的齊次線性微分方程為
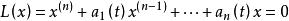非齊次線性微分方程
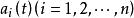非齊次線性微分方程其中及f(t)都是R上的連續函式。
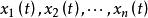非齊次線性微分方程
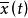非齊次線性微分方程如果是齊次方程的一個基本解組，而是非齊次方程的某個解，則非齊次方程的通解可以表示為
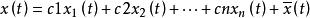非齊次線性微分方程其中c1,c2,...,cn是任意常數。
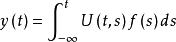非齊次線性微分方程
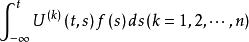非齊次線性微分方程 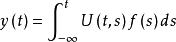非齊次線性微分方程若n階非齊次線性微分方程的柯西函式U(t,s)及U^(k)(t,s)(k=1,2,...,n)均連續，函式及都是一致收斂的，則函式是非齊次線性微分方程的一個解 。
