一般形式
二階微分方程的一般形式是
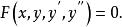二階微分方程其中，x是自變數，y是未知函式，y'是y的一階導數，y''是y的二階導數。
可降階方程
在有些情況下，可以通過適當的變數代換，把二階微分方程化成一階微分方程來求解。具有這種性質的微分方程稱為可降階的微分方程，相應的求解方法稱為降階法。下面介紹三種容易用降階法求解的二階微分方程。
1）y''=f(x)型
方程特點：右端僅含有自變數x，逐次積分即可得到通解，對二階以上的微分方程也可類似求解。
例1 求方程y''=e -cosx的通解。
解：原方程兩邊積分兩次，得通解
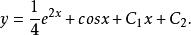二階微分方程其中，C，C為任意常數。
2）y''=f(x,y')型
方程特點：右端函式表達式中不含有未知函式y。
由於y'也是x的未知函式，可設p(x)=y'，則原方程可降階為
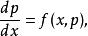二階微分方程這是關於p的一階微分方程，可求通解。
3）y''=f(y,y')型
方程特點：右端函式表達式中不含有自變數x。
令y'=p(y)，利用複合函式求導法則
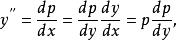二階微分方程原方程變為關於y，p的一階方程
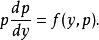二階微分方程線性微分方程
一般形如
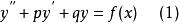二階微分方程
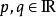二階微分方程（其中，f(x)是x的函式）的方程稱為 二階常係數線性微分方程。
當f(x)=0時，方程
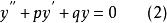二階微分方程稱為 二階常係數線性齊次微分方程；否則，方程（1）稱為 二階常係數線性非齊次微分方程。
1）二階常係數線性 齊次微分方程的解
定理1（線性齊次微分方程通解的結構定理）如果函式y(x)與y(x)是(2)的兩個線性無關的解，則函式
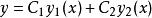二階微分方程是齊次方程（2）的通解。（其中，C、C為兩個獨立的任意常數）
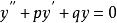二階微分方程微分方程 的通解與其特徵根的關係見下表1。
表1 齊次微分方程通解與其特徵根的關係2）二階常係數線性 非齊次微分方程的解
定理2（線性非齊次微分方程通解的結構定理）如果y是非齊次微分方程（1）的一個特解，而y*是對應的齊次微分方程（2）的通解，則y=y+y*是方程（1）的通解。
對於比較簡單的情形，可以用觀察法找特解。但對於比較複雜的情形就不太容易了。為此，下面對於f(x)的幾種常見形式，以表2列出找其特解的方法（待定係數法）（表2中P(x)=a+ax+ax +...+ax 為已知的多項式）。
表2 非齊次微分方程特解形式與f(x)的關係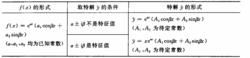
表2 非齊次微分方程特解形式與f(x)的關係