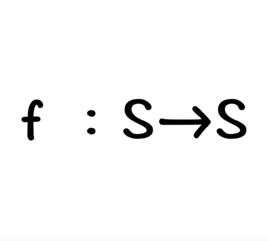簡介
設 S 是集合,函式 f :S→S 稱為 S 上的一個一元運算。
示例
(1) 求數的相反數是整數集合 Z 、有理數集合 Q 和實數集合 R 上的一元運算;
(2) 求數的倒數是非零有理數集和非零實數集上的一元運算;
(3) 求複數的共軛複數是複數集合 C 上的一元運算;
(4) 在冪集合 P(S) 上,如果規定全集為 S ,則求集合的絕對補運算是 P(S) 上的一元運算;
(5) 設集合 S 上所有雙射函式滿足一定條件,則求雙射函式的反函式是 A 上的一元運算;
(6) 在 n(n≥2) 階實數集合 (R) 上,求矩陣的轉置矩陣是 (R) 上的一元運算。
註:驗證 S 上一種運算是否為一元運算主要應檢驗兩點:
(1) S 中任何元素都能進行這種運算,且運算結果是唯一的;
(2) S 中任何元素進行運算的結果都仍在 S 中,即 S 對運算是封閉的。
運算
[operation]
運算亦稱演算,數學的基本概念之一,指使的一些計算規則,算術中有加、減、乘、除、乘方、開方六種運算,其中加、減、乘、除是從兩個已知數得出第三個數的運算,稱為二元運算;乘方、開方是從一個已知數得出另一個數的運算,稱為一元運算,得出的數稱為運算結果,若已知運算結果,反求原數(一元運算)或兩個原數之一(二元運算)的計算規則,稱為原運算的逆運算,此時把原運算稱為直接運算,一元運算的逆運算仍是一元運算;對二元運算的逆運算,總假定兩個原數之一也是已知數,因此,逆運算仍是從兩個已知數得出一個數(未知的一個原數)的運算,即仍是二元運算,一個運算的逆運算是以原運算為其逆運算的,即這兩個運算是互逆的,算術中通常把加法、乘法和乘方看做直接運算,而把減法、除法和開方分別看成是它們的逆運算,這樣三對運算是互逆的。