高斯消元法

數學上，高斯消元法（或譯：高斯消去法），是線性代數規劃中的一個算法，可用來為線性方程組求解。但其算法十分複雜，不常用於加減消元法，求出矩陣的秩，以及求出可逆方陣的逆矩陣。不過，如果有過百萬條等式時，這個算法會十分省時。一些極大的方程組通常會用疊代法以及花式消元來解決。當用於一個矩陣時，高斯消元法會產生出一個“行梯陣式”。高斯消元法可以用在電腦中來解決數千條等式及未知數。亦有一些方法特地用來解決一些有特別排列的係數的方程組。

基本信息

• 中文名：高斯消元法
• 英文名：Gauss Elimination

• 命 名：高斯
• 最早出現：《九章算術》
• 類 別：線性代數算法
• 其他套用：找出逆矩陣

歷史

該方法以數學家高斯命名，由拉布扎比.伊丁特改進，發表於法國但最早出現於中國古籍《九章算術》，成書於約公元前150年。

例子

高斯消元法

這個算法的原理是：

首先，要將L1 以下的等式中的x 消除，然後再將L2 以下的等式中的y 消除。這樣可使整個方程組變成一個三角形似的格式。通常人或電腦在套用高斯消元法的時候，不會直接寫出方程組的等式來消去未知數，反而會使用矩陣來計算。之後再將已得出的答案一個個地代入已被簡化的等式中的未知數中，就可求出其餘的答案了。

在剛才的例子中，我們將二分之三 L1和L2相加，就可以將L2 中的X消除了。然後再將L1 和L3相加，就可以將L3 中的x 消除。

高斯消元法可用來找出下列方程組的解或其解的限制：

2x + y - z = 8 (L1)

-3x - y + 2z = -11 (L2)

-2x + y + 2z = -3 (L3)

我們可以這樣寫：

L2 + 3/2 L1→ L2

L3 + L1 → L3

結果就是：

2x + y - z = 8

1/2 y + 1/2 z = 1

2y + z = 5

現在將 − 4L2 和L3 相加，就可將L3 中的y 消除：

L3 + -4 L2 → L3

其結果是：

2x + y - z = 8

1/2y + 1/2z = 1

-z = 1

這樣就完成了整個算法的初步，一個三角形的格式(指:變數的格式而言,上例中的變數各為3,2,1個)出現了。

第二步，就是由尾至頭地將已知的答案代入其他等式中的未知數。第一個答案就是：

z = -1

然後就可以將z 代入L2 中，立即就可得出第二個答案：

y = 3

之後，將z 和y 代入L1 之中，最後一個答案就出來了：

x = 2

就是這樣，這個方程組就被高斯消元法解決了。

高斯消元法

這種算法可以用來解決所有線性方程組。即使一個方程組不能被化為一個三角形的格式，高斯消元法仍可找出它的解。例如在第一步化簡後，L2 及L3 中沒有出現任何y ，沒有三角形的格式，照著高斯消元法而產生的格式仍是一個行梯陣式。這情況之下，這個方程組會有超過一個解，當中會有至少一個變數作為答案。每當變數被鎖定，就會出現一個解。

以下就是使用矩陣來計算的例子：

2 1 -1 8

-3 -1 2 -11

-2 1 2 -3

跟著以上的方法來運算，這個矩陣可以轉變為以下的樣子：

2 1 -1 8

0 1/2 1/2 1

0 0 -1 1

這矩陣叫做“行梯列式”。

最後，可以利用同樣的算法產生以下的矩陣，便可把所得出的解或其限制簡明地表示出來：

1 0 0 2

0 1 0 3

0 0 1 -1

最後這矩陣叫做“簡化行梯列式”，亦是高斯－約當消元法指定的步驟。

其他套用

高斯消元法

找出逆矩陣

高斯消元法可以用來找出一個可逆矩陣的逆矩陣。設A 為一個N * N的矩陣，其逆矩陣可被兩個分塊矩陣表示出來。將一個N * N單位矩陣 放在A 的右手邊，形成一個N * 2N的分塊矩陣B = [A,I] 。經過高斯消元法的計算程式後，矩陣B 的左手邊會變成一個單位矩陣I ，而逆矩陣A ^(-1) 會出現在B 的右手邊。

假如高斯消元法不能將A 化為三角形的格式，那就代表A 是一個不可逆的矩陣。

套用上，高斯消元法極少被用來求出逆矩陣。高斯消元法通常只為線性方程組求解。

計出秩的基本算法

高斯消元法可套用在任何m * n的矩陣A。在不可減去某數的情況下，我們都只有跳到下一行。以一個6 * 9的矩陣作例，它可以變化為一個行梯陣式：

1 * 0 0 * * 0 * 0

0 0 1 0 * * 0 * 0

0 0 0 1 * * 0 * 0

0 0 0 0 0 0 1 * 0

0 0 0 0 0 0 0 0 1

0 0 0 0 0 0 0 0 0

而矩陣中的 *' 是一些數字。這個梯陣式的矩陣T 會有一些關於A的資訊：

A 的秩是5，因為T 有5行非0的行；

A 的列的向量空間，可從A 的第1、3、4、7和9列中得知，其數值在矩陣T 之中；

矩陣中的 *' 表示了A 的列可怎樣寫為列中的數的組合。

分析

高斯消元法的算法複雜度是O（n3）；這就是說，如果係數矩陣的是n × n，那么高斯消元法所需要的計算量大約與n3成比例。

高斯消元法可用在任何域中。

高斯消元法對於一些矩陣來說是穩定的。對於普遍的矩陣來說，高斯消元法在套用上通常也是穩定的，不過亦有例外。

偽代碼

高斯消元法的其中一種偽代碼：

這個算法和之前談及的有點兒不同，它由絕對值最大的部分開始做起，這樣可以改善算法上的穩定性。將經過調換後的第一列作為起點，這算法由左至右地計算。每作出以下兩個步驟，才跳到下一列：

高斯消元法

1.定出每列的最後一個非0的數，將每行的數字除以該數，使到每行的第一個數成為1；

2.將每行的數字減去第一行的第一個數的某個倍數。

所有步驟完成後，這個矩陣會變成一個行梯陣式，再用代入法就可解決這個方程組。

線性方程組其實是相當容易解決的，基本的思想就是消元。但是當未知數較多時，解起來也蠻頭疼的。在這裡向大家介紹高斯消元法。例如解如下四元一次方程組：

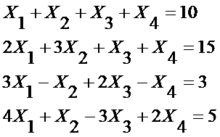高斯消元法

高斯消元法

除去各未知數，將各數排在一起，成為矩陣：

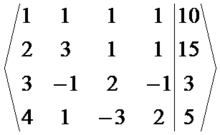高斯消元法

為方便起見，用r2+r1表示把第一行各數加到第二行對應數上。

r2-2*r1, r3-3*r1, r4-4*r1, 可得：

r3+4*r2, r4+3*r2, 可得：

r4-2*r3, 可得：

化為方程組形式則為：

從而，可得：

X4=4

X3=3

X2=2

X1=1.

說明：對於矩陣採取的變換的合理性，可對照相應方程組的變換加以理解。