來源
一元四次方程求根公式費拉里與一元四次方程的解法 卡當在《重要的藝術》一書中公布了塔塔利亞發現的一元三次方程求根公式之後，塔塔利亞譴責卡當背信棄義，提出要與卡當進行辯論與比賽。這場辯論與比賽在米蘭市的教堂進行，代表卡當出場的是卡當的學生費拉里。 費拉里(Ferrari L.,1522~1565)出身貧苦，少年時代曾作為卡當的僕人。卡當的數學研究引起了他對數學的熱愛，當其數學才能被卡當發現後，卡當就收他作了學生。 費拉里代替卡當與塔塔利亞辯論並比賽時，風華正茂，他不僅掌握了一元三次方程的解法，而且掌握了一元四次方程的解法，因而在辯論與比賽中取得了勝利，並由此當上了波倫亞大學的數學教授。 一元四次方程的求解方法，是受一元三次方程求解方法的啟發而得到的。一元三次方程是在進行了巧妙的換元之後，把問題歸結成了一元二次方程從而得解的。於是，如果能夠巧妙地把一元四次方程轉化為一元三次方程或一元二次方程，就可以利用已知的公式求解了。
費拉里法
費拉里的方法是這樣的：方程兩邊同時除以最高次項的係數可得 x^4+bx^3+cx^2+dx+e=0 (1)移項可得 x^4+bx^3=-cx^2-dx-e (2) 兩邊同時加上(1/2bx)^2 ，可將（2）式左邊配成完全平方，方程成為 (x^2+1/2bx)^2=(1/4b^2-c)x^2-dx-e (3) 在（3）式兩邊同時加上(x^2+1/2bx)y+1/4y^2 可得 [(x^2+1/2bx)+1/2y]^2= (1/4b^2-c+y)x^2+(1/2by-d)x+1/4y^2-e (4) （4）式中的y是一個參數。當（4）式中的x為原方程的根時，不論y取什麼值，（4）式都應成立。特別，如果所取的y值使（4）式右邊關於x的二次三項式也能變成一個完全平方式，則對（4）對兩邊同時開方可以得到次數較低的方程。 為了使（4）式右邊關於x的二次三項式也能變成一個完全平方式，只需使它的判別式變成0，即 (1/2by-d)^2-4(1/4b^2-c+y)(1/4y^2-e)=0 (5) 這是關於y的一元三次方程，可以通過塔塔利亞公式來求出y應取的實數值。 把由（5）式求出的y值代入（4）式後，（4）式的兩邊都成為完全平方，兩邊開方，可以得到兩個關於x的一元二次方程。解這兩個一元二次方程，就可以得出原方程的四個根。 費拉里發現的上述解法的創造性及巧妙之處在於：第一次配方得到（3）式後引進參數y，並再次配方把（3）式的左邊配成含有參數y的完全平方，即得到（4）式，再利用（5）式使（4）的右邊也成為完全平方，從而把一個一元四次方程的求解問題化成了一個一元三次方程及兩個一元二次方程的求解問題。
誤用：
不幸的是，就象塔塔利亞發現的一元三次方程求根公式被誤稱為卡當公式一樣，費拉里發現的一元四次方程求解方法也曾被誤認為是波培拉發現的。
置換群法
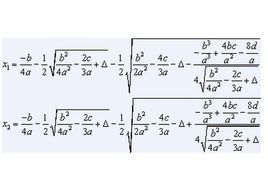
解法見圖片
一元四次方程求根公式
一元四次方程求根公式說明:X1，X2，X3是某個三次方程的對稱多項式(X1+X2+X3，X1*X2+X2*X3+X3*X1，X1*X2*X3均可求)，利用三次方程求根公式解出X1,X2,X3;又有X=x1+x2+x3+x4=ω1，接下來根據X,X1,X2,X3解x1,x2,x3,x4
盛金公式
將置換群解法與盛金公式綜合，會更簡便。解法：
一元四次方程求根公式若ax^4+bx^3+cx^2+dx+e=0 令 D=-(3b^2-8ac)
E=3b^4+16a^2c^2-16ab^2c+16a^2bd-64a^3e F=-(b^3-4abc+8a^2d)^2
A=D^2-3E,B=DE-9F,C=E^2-3DF,Δ=B^2-4AC
1.若D=E=F=0，則方程有一個四重根。則
x1=x2=x3=x4=-b/4a=-2c/3b=-3c/2d=-4d/e
2.若A=B=C=0，且DEF不為0，則方程有一個三重根。則
x1=-b/4a-F/4aD x2=x3=x4=-b/4a+3F/4aD
3.若E=F=0，D不為零，則方程有兩對重根。
x1=x2=(-b+(-D)^(1/2))/4a x3=x4=(-b-(-D)^(1/2))/4a
4.若Δ=0，A不為零，則方程只有一對重根。
令X1=-D+B/A,X2=-B/2A,則
x1=(-b+X1^(1/2)+2X2^(1/2))/4a x2=(-b+X1^(1/2)-2X2^(1/2))/4a x3=x4=(-b+X1^(1/2))/4a
5.若Δ<0,令T=arccos[(2AD-3B)/2A^(3/2)]
y1=-(D+2A^(1/2)cos(T/3)
y2=-(D+2A^(1/2)cos(T/3+2π/3)
y3=-(D+2A^(1/2)cos(T/3-2π/3)
x1=(-b+y1^(1/2)+y2^(1/2)+y3^(1/2))/4a
x2=(-b+y1^(1/2)-y2^(1/2)-y3^(1/2))/4a
x3=(-b-y1^(1/2)-y2^(1/2)+y3^(1/2))/4a
x4=(-b-y1^(1/2)+y2^(1/2)-y3^(1/2))/4a
6.若Δ>0
Y1=AD+(3/2)(-B+(B^2-4AC)^(1/2))
Y2=AD+(3/2)(-B-(B^2-4AC)^(1/2))
Z1=(-2D-Y1^(1/3)-Y2^(1/3))/6
Z2=3^(1/2)(Y1^(1/3)-Y2^(1/3))/6
Z=-(-D+Y1^(1/3)+Y2^(1/3))/3
W1=(2Z1+2(Z1^2+Z2^2)^(1/2))^(1/2)
W2=(-2Z1+2(Z1^2+Z2^2)^(1/2))^(1/2)
x1=(-b+Z^(1/2)+2W1)/4a x2=(-b+Z^(1/2)-2W1)/(4a)
x3=(-b-Z^(1/2)-2W2)/4a x4=(-b-Z^(1/2)+2W2)/(4a)
