簡介
回歸這一術語最早來源於生物遺傳學，由高爾頓（Francis Galton）引入。
回歸的現代解釋：回歸分析是研究某一變數（因變數）與另一個或多個變數（解釋變數、自變數）之間的依存關係，用解釋變數的已知值或固定值來估計或預測因變數的總體平均值 。
因變數：Y
自變數：X或X1，X2，…等
高爾頓的興趣在於尋找為什麼總體身高分布趨向穩定。現在我們所關心的已不是這個問題，而是想知道在已知父親身高的情況下，兒子的身高的平均變化如何。換句話說，就是已知父親身高來預測兒子的平均身高。
定義
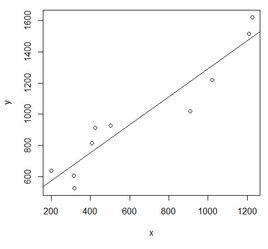
一元線性回歸分析預測法，是根據自變數x和因變數Y的相關關係，建立x與Y的線性回歸方程進行預測的方法。由於市場現象一般是受多種因素的影響，而並不是僅僅受一個因素的影響。所以套用一元線性回歸分析預測法，必須對影響市場現象的多種因素做全面分析。只有當諸多的影響因素中，確實存在一個對因變數影響作用明顯高於其他因素的變數，才能將它作為自變數，套用一元相關回歸分析市場預測法進行預測 。
一元線性回歸分析法的預測模型為：
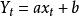一元線性回歸式中， x代表t期自變數的值；
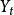一元線性回歸代表t期因變數的值；
a、b代表一元線性回歸方程的參數。
a、b參數由下列公式求得（用代表）：
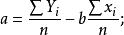一元線性回歸
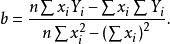一元線性回歸一元線性回歸模型
建立模型
1、選取一元線性回歸模型的變數 ；
2、繪製計算表和擬合散點圖 ；
3、計算變數間的回歸係數及其相關的顯著性 ；
4、回歸分析結果的套用 。
模型的檢驗
1、經濟意義檢驗：就是根據模型中各個參數的經濟含義，分析各參數的值是否與分析對象的經濟含義相符；
2、回歸標準差檢驗；
3、擬合優度檢驗；
4、回歸係數的顯著性檢驗。
