多元線性回歸的計算模型
一元線性回歸是一個主要影響因素作為自變數來解釋因變數的變化，在現實問題研究中，因變數的變化往往受幾個重要因素的影響，此時就需要用兩個或兩個以上的影響因素作為自變數來解釋因變數的變化，這就是多元回歸亦稱多重回歸。當多個自變數與因變數之間是線性關係時，所進行的回歸分析就是多元線性回歸。
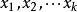多元線性回歸分析預測法設y為因變數， 為自變數，並且自變數與因變數之間為線性關係時，則多元線性回歸模型為：
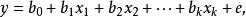多元線性回歸分析預測法
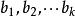多元線性回歸分析預測法
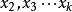多元線性回歸分析預測法其中，b為常數項， 為回歸係數，b為 固定時，x每增加一個單位對y的效應，即x對y的偏回歸係數；同理b為x,x固定時，x每增加一個單位對y的效應，即，x對y的偏回歸係數，等等。如果兩個自變數x,x同一個因變數y呈線相關時，可用二元線性回歸模型描述為：y=b+bx+bx+e。
建立多元性回歸模型時，為了保證回歸模型具有優良的解釋能力和預測效果，應首先注意自變數的選擇，其準則是：
(1)自變數對因變數必須有顯著的影響，並呈密切的線性相關；
(2)自變數與因變數之間的線性相關必須是真實的，而不是形式上的；
(3)自變數之間應具有一定的互斥性，即自變數之間的相關程度不應高於自變數與因變數之因的相關程度；
(4)自變數應具有完整的統計數據，其預測值容易確定。
多元性回歸模型的參數估計，同一元線性回歸方程一樣，也是在要求誤差平方和()為最小的前提下，用最小二乘法求解參數。以二線性回歸模型為例，求解回歸參數的標準方程組為：
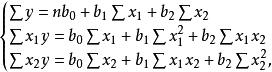多元線性回歸分析預測法解此方程可求得b,b,b的數值。亦可用下列矩陣法求得
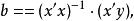多元線性回歸分析預測法即
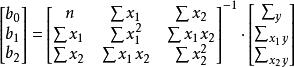多元線性回歸分析預測法多元線性回歸模型的檢驗
多元性回歸模型與一元線性回歸模型一樣，在得到參數的最小二乘法的估計值之後，也需要進行必要的檢驗與評價，以決定模型是否可以套用。
1.擬合程度的測定。
與一元線性回歸中可決係數r 相對應，多元線性回歸中也有多重可決係數r ，它是在因變數的總變化中，由回歸方程解釋的變動(回歸平方和)所占的比重，R 越大，回歸方各對樣本數據點擬合的程度越強，所有自變數與因變數的關係越密切。計算公式為：
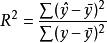多元線性回歸分析預測法
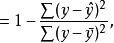多元線性回歸分析預測法其中
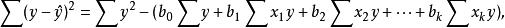多元線性回歸分析預測法
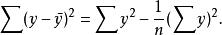多元線性回歸分析預測法2.估計標準誤差
估計標準誤差，即因變數y的實際值與回歸方程求出的估計值之間的標準誤差，估計標準誤差越小，回歸方程擬合程度越程。
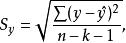多元線性回歸分析預測法
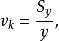多元線性回歸分析預測法其中，k為多元線性回歸方程中的自變數的個數。
3.回歸方程的顯著性檢驗
回歸方程的顯著性檢驗，即檢驗整個回歸方程的顯著性，或者說評價所有自變數與因變數的線性關係是否密切。能常採用F檢驗，F統計量的計算公式為：
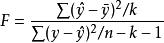多元線性回歸分析預測法
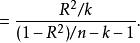多元線性回歸分析預測法根據給定的顯著水平a,自由度(k,n-k-1)查F分布表，得到相應的臨界值F，若F>F，則回歸方程具有顯著意義，回歸效果顯著；F<F，則回歸方程無顯著意義，回歸效果不顯著。
4.回歸係數的顯著性檢驗
在一元線性回歸中，回歸係數顯著性檢驗(t檢驗)與回歸方程的顯著性檢驗(F檢驗)是等價的，但在多元線性回歸中，這個等價不成立。t檢驗是分別檢驗回歸模型中各個回歸係數是否具有顯著性，以便使模型中只保留那些對因變數有顯著影響的因素。檢驗時先計算統計量t；然後根據給定的顯著水平a,自由度n-k-1查t分布表，得臨界值t或t,t>t−a或t，則回歸係數b與0有顯著關異，反之，則與0無顯著差異。統計量t的計算公式為：
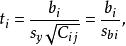多元線性回歸分析預測法其中，C是多元線性回歸方程中求解回歸係數矩陣的逆矩陣(x'x)的主對角線上的第j個元素。對二元線性回歸而言，可用下列公式計算：
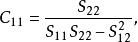多元線性回歸分析預測法
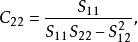多元線性回歸分析預測法其中
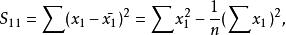多元線性回歸分析預測法
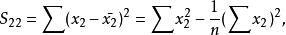多元線性回歸分析預測法
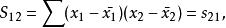多元線性回歸分析預測法
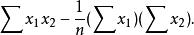多元線性回歸分析預測法5.多重共線性判別
若某個回歸係數的t檢驗通不過，可能是這個係數相對應的自變數對因變數的影平不顯著所致，此時，應從回歸模型中剔除這個自變數，重新建立更為簡單的回歸模型或更換自變數。也可能是自變數之間有共線性所致，此時應設法降低共線性的影響。
多重共線性是指在多元線性回歸方程中，自變數之間有較強的線性關係，這種關係若超過了因變數與自變數的線性關係，則回歸模型的穩定性受到破壞，回歸係數估計不準確。需要指出的是，在多元回歸模型中，多重共線性的難以避免的，只要多重共線性不太嚴重就行了。判別多元線性回歸方程是否存在嚴懲的多重共線性，可分別計算每兩個自變數之間的可決係數r，若r >R 或接近於R，則應設法降低多重線性的影響。亦可計算自變數間的相關係數矩陣的特徵值的條件數k= λ/ λ(λ為最大特徵值，λ為最小特徵值),k<100，則不存在多重點共線性；若100≤k≤1000，則自變數間存在較強的多重共線性，若k>1000，則自變數間存在嚴重的多重共線性。降低多重共線性的辦法主要是轉換自變數的取值，如變絕對數為相對數或平均數，或者更換其他的自變數。
6.D.W檢驗
當回歸模型是根據動態數據建立的，則誤差項e也是一個時間序列，若誤差序列諸項之間相互獨立，則誤差序列各項之間沒有相關關係，若誤差序列之間存在密切的相關關係，則建立的回歸模型就不能表述自變數與因變數之間的真實變動關係。D.W檢驗就是誤差序列的自相關檢驗。檢驗的方法與一元線性回歸相同。
