介紹
ode是Matlab專門用於解微分方程的功能函式。該求解器有變步長(variable-step)和定步長(fixed-step)兩種類型。不同類型有著不同的求解器,其中ode45求解器屬於變步長的一種,採用Runge-Kutta算法;其他採用相同算法的變步長求解器還有ode23。
ode45表示採用四階-五階Runge-Kutta算法,它用4階方法提供候選解,5階方法控制誤差,是一種自適應步長(變步長)的常微分方程數值解法,其整體截斷誤差為(Δx)^5。解決的是Nonstiff(非剛性)常微分方程。
ode45是解決數值解問題的首選方法,若長時間沒結果,應該就是剛性的,可換用ode15s試試。
語法
[T,Y] = ode45(odefun,tspan,y0)
[T,Y] = ode45(odefun,tspan,y0,options)
[T,Y,TE,YE,IE] = ode45(odefun,tspan,y0,options)
sol = ode45(odefun,[t0tf],y0...)
[T,Y] = ode45(odefun,tspan,y0)
odefun 是函式句柄,可以是函式檔案名稱,匿名函式句柄或內聯函式名
tspan 是區間 [t0 tf] 或者一系列散點[t0,t1,...,tf]
y0 是初始值向量
T 返回列向量的時間點
Y 返回對應T的求解列向量
[T,Y] = ode45(odefun,tspan,y0,options)
options 是求解參數設定,可以用odeset在計算前設定誤差,輸出參數,事件等
[T,Y,TE,YE,IE] =ode45(odefun,tspan,y0,options)
在設定了事件參數後的對應輸出
TE 事件發生時間
YE 事件發生時之答案
IE 事件函式消失時之指針i
sol =ode45(odefun,[t0 tf],y0...)
sol 結構體輸出結果
示例
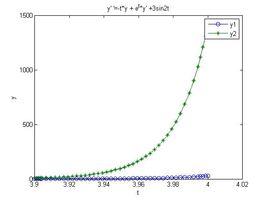
求解一階常微分方程
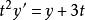 ode45
ode45需要求解的一階常微分方程:
odefun=@(t,y) (y+3*t)/t^2; %定義函式
tspan=[1 4]; %求解區間
y0=-2; %初值
[t,y]=ode45(odefun,tspan,y0);
plot(t,y) %作圖
title('t^2y''=y+3t,y(1)=-2,1<t<4')
legend('t^2y''=y+3t')
xlabel('t')
ylabel('y')
% 精確解
% dsolve('t^2*Dy=y+3*t','y(1)=-2')
% ans =一階求解結果圖
% (3*Ei(1) - 2*exp(1))/exp(1/t) - (3*Ei(1/t))/exp(1/t)
求解高階常微分方程
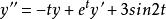 ode45
ode45需要求解的高階常微分方程:
求解的關鍵是將高階轉為一階,odefun的書寫.
F(y,y',y''...y(n-1),t)=0用變數替換,y1=y,y2=y'...注意odefun方程定義為行向量
dxdy=[y(1),y(2)....]
程式:
function Testode45
tspan=[3.9 4.0]; %求解區間
y0=[2 8]; %初值
[t,x]=ode45(@odefun,tspan,y0);
plot(t,x(:,1),'-o',t,x(:,2),'-*')
legend('y1','y2')
title('y'' ''=-t*y + e^t*y'' +3sin2t')
xlabel('t')
ylabel('y')
function y=odefun(t,x)
y=zeros(2,1); % 列向量
y(1)=x(2);
y(2)=-t*x(1)+exp(t)*x(2)+3*sin(2*t);
end
end