EM算法
在統計計算中,最大期望(EM)算法是在機率(probabilistic)模型中尋找參數最大似然估計或者最大後驗估計的算法,其中機率模型依賴於無法觀測的隱藏變數(Latent Variable)。最大期望經常用在機器學習和計算機視覺的數據聚類(Data Clustering)領域。
最大期望算法經過兩個步驟交替進行計算:
第一步是計算期望(E),利用對隱藏變數的現有估計值,計算其最大似然估計值;
第二步是最大化(M),最大化在 E 步上求得的最大似然值來計算參數的值。
M 步上找到的參數估計值被用於下一個 E 步計算中,這個過程不斷交替進行。
總體來說,EM的算法流程如下:
1.初始化分布參數
2.重複直到收斂:
E步驟:估計未知參數的期望值,給出當前的參數估計。
M步驟:重新估計分布參數,以使得數據的似然性最大,給出未知變數的期望估計。
算法簡述
疊代使用EM步驟,直至收斂。
可以有一些比較形象的比喻說法把這個算法講清楚。比如說食堂的大師傅炒了一份菜,要等分成兩份給兩個人吃,顯然沒有必要拿來天平一點一點的精確的去稱分量,最簡單的辦法是先隨意的把菜分到兩個碗中,然後觀察是否一樣多,把比較多的那一份取出一點放到另一個碗中,這個過程一直疊代地執行下去,直到大家看不出兩個碗所容納的菜有什麼分量上的不同為止。EM算法就是這樣,假設我們估計知道A和B兩個參數,在開始狀態下二者都是未知的,並且知道了A的信息就可以得到B的信息,反過來知道了B也就得到了A。可以考慮首先賦予A某種初值,以此得到B的估計值,然後從B的當前值出發,重新估計A的取值,這個過程一直持續到收斂為止。
EM 算法是 Dempster,Laind,Rubin 於 1977 年提出的求參數極大似然估計的一種方法,它可以從非完整數據集中對參數進行 MLE 估計,是一種非常簡單實用的學習算法。這種方法可以廣泛地套用於處理缺損數據,截尾數據,帶有噪聲等所謂的不完全數據(incomplete data)。
假定集合Z = (X,Y)由觀測數據 X 和未觀測數據Y 組成, X 和Z = (X,Y)分別稱為不完整數據和完整數據。假設Z的聯合機率密度被參數化地定義為P(X,Y|Θ),其中Θ 表示要被估計的參數。Θ 的最大似然估計是求不完整數據的對數似然函式L(X;Θ)的最大值而得到的:
L(Θ; X )= log p(X |Θ) = ∫log p(X ,Y |Θ)dY ;
EM算法包括兩個步驟:由E步和M步組成,它是通過疊代地最大化完整數據的對數似然函式Lc( X;Θ )的期望來最大化不完整數據的對數似然函式,其中:
Lc(X;Θ) =log p(X,Y |Θ) ;
假設在算法第t次疊代後Θ 獲得的估計記為Θ(t ) ,則在(t+1)次疊代時,
E-步:計算完整數據的對數似然函式的期望,記為:
Q(Θ |Θ (t) ) = E{Lc(Θ;Z)|X;Θ(t) };
M-步:通過最大化Q(Θ |Θ(t) ) 來獲得新的Θ 。
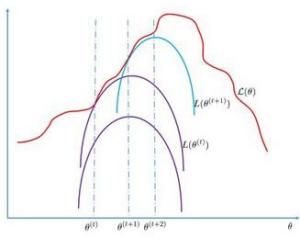
通過交替使用這兩個步驟,EM算法逐步改進模型的參數,使參數和訓練樣本的似然機率逐漸增大,最後終止於一個極大點。直觀地理解EM算法,它也可被看作為一個逐次逼近算法:事先並不知道模型的參數,可以隨機的選擇一套參數或者事先粗略地給定某個初始參數λ0 ,確定出對應於這組參數的最可能的狀態,計算每個訓練樣本的可能結果的機率,在當前的狀態下再由樣本對參數修正,重新估計參數λ ,並在新的參數下重新確定模型的狀態,這樣,通過多次的疊代,循環直至某個收斂條件滿足為止,就可以使得模型的參數逐漸逼近真實參數。
EM算法的主要目的是提供一個簡單的疊代算法計算後驗密度函式,它的最大優點是簡單和穩定,但容易陷入局部最優