簡介
Sobolev空間 Sobolev空間對於數學函式的光滑性有很多種。最基本的要求可能就是函式要連續，更進一步的要求是導數（因為可微函式也是連續的），再強一些的概念是導數的連續性（這些函式稱為— 參看光滑函式）。可微函式在很多領域相當重要，特別是在微分方程中。在二十世紀，人們發現函式空間不是研究微分方程的解的恰當的空間。
Sobolev空間而索博列夫空間正是空間的替代品，用於研究偏微分方程的解。
技術性討論
Sobolev空間
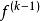Sobolev空間我們從最簡單情況下的索博列夫空間開始，也就是單位圓上的一維情況。在這個情況下，索博列夫空間定義為 L的子集，使得 f和它的直到 k階的導數有一個有限的 L範數，對於某個給定的 p≥ 1。定義正確意義上的導數時必須小心。在這個一維問題中，假設是幾乎處處可微並且等於其導數的勒貝格積分（這可以排除康托函式這樣的例子）就足夠了。
按照這個定義，索博列夫空間有一個自然的範數,
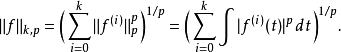Sobolev空間
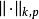Sobolev空間 Sobolev空間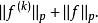
Sobolev空間賦予了範數的是一個完備空間。實際上只要取序列中的第一項和最後一項就可以了，也即，如下的範數和上述範數等價。
例子
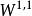Sobolev空間
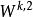Sobolev空間有些索博列夫空間有簡單的表述。例如，在一維情況，就是絕對連續函式空間，而 W是李普希茲函式空間。還有，可以自然地用其傅立葉級數的術語定義，也就是
Sobolev空間其中是 f的傅立葉級數。和前面一樣，可以採用等價的範數
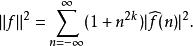Sobolev空間兩個表達都可以從帕塞瓦爾定理以及微分等價於傅立葉係數乘以 in這個事實導出。
非整數k情況
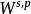Sobolev空間
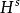Sobolev空間為避免混淆，在討論不是整數的 k的時候，我們通常用 s來取代它，也即或者。
p等於2
p= 2的情形是最簡單的情形，因為傅立葉表述可以直接推廣。我們定義範數為
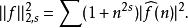Sobolev空間 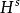Sobolev空間而索博列夫空間為具有有限範數的函式的空間。
分數階微分
如果 p不是2，就採取類似的方法。在這個情況下帕塞瓦爾定理不再成立，但是微分還是對應於在傅立葉域中的乘法，並且可以推廣到非整數階。因此，可以定義一個分數階微分的運算元其階為s，如下所示
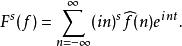Sobolev空間
Sobolev空間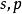
Sobolev空間換句話說，取傅立葉變換，乘以再取逆傅立葉變換（定義為傅立葉－乘法－逆傅立葉的運算元稱為乘子，這本身也是一個研究主題）。這使得我們可以定義的索博列夫範數如下
Sobolev空間而且，跟平常一樣，索博列夫空間是有有限索博列夫範數的函式的空間。
復插值
獲取“分數索博列夫空間”的另一個辦法是採用復插值。復插值是一個通用的技術：對於任何0 ≤ t ≤ 1 和巴拿赫空間 X及 Y，且這二者都包含於某個更大的巴拿赫空間中，我們可以創建“過渡空間”，記為[ X, Y]。（後面將會討論到一個不同的方法，所謂的實插值方法，它對於跡的分類的索博列夫理論有重要的意義）。
多維情況
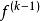Sobolev空間
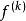Sobolev空間現在考慮在 R及其子集上的索博列夫空間。從圓到線的變化只涉及傅立葉公式的技術細節 — 基本上就是將傅立葉級數變為傅立葉變換，將求和變為積分。到多維情況的轉換有更大的難度，從定義就開始變化。是的積分這個條件無法一般化，而最簡單的解決辦法是考慮分布理論意義下的導數。
由此可以得到一個形式化的定義。令 D為 R中開集。定義索博列夫空間
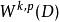Sobolev空間
Sobolev空間為定義於 D上的函式 f的族，使得對於滿足下式的每個多重索引
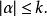Sobolev空間
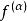Sobolev空間是一個函式，且
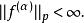Sobolev空間在它上面的一個合適的範數是所有這樣的α上的那些 L範數的和。它是完備的，因此是一個巴拿赫空間。
實際上，這個方法在一維也成立，並且和前面分數階微分中所述並無多大區別。
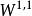Sobolev空間
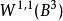Sobolev空間
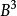Sobolev空間 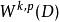Sobolev空間在多維情況，有些結果不再成立，例如，只包含連續函式。例如，1/| x|屬於，其中是三維的單位球。對於足夠大的 k，將只包含連續函式，但是對於哪個 k才夠取決於 p以及維數這二者。
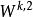Sobolev空間但是， W和的表述在做了必要的修改之後還是成立的。
索博列夫嵌入
Sobolev空間
Sobolev空間 Sobolev空間索博列夫空間是的子集。一個很自然的問題是:有沒有其它的 L空間包含？索博列夫嵌入定理給出一個簡單的表達（參看）:
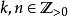Sobolev空間
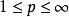Sobolev空間定理:令且。則如下命題成立:
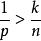Sobolev空間
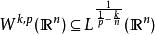Sobolev空間若則（作為集合）。而且，包含關係是一個有界運算元。
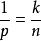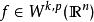Sobolev空間
Sobolev空間
Sobolev空間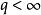
Sobolev空間若則所有有緊支撐的函式是的元素，其中。
