定理內容
Ramsey定理的通俗表述：
6 個人中至少存在3人相互認識或者相互不認識。
該定理等價於證明這6個頂點的完全圖的邊，用紅、藍二色任意著色，必然至少存在一個紅色邊三角形，或藍色邊三角形。
註：這個定理以弗蘭克·普倫普頓·拉姆齊命名，1930年他在論文On a Problem in Formal Logic （《形式邏輯上的一個問題》）證明了R(3,3)=6。
證明
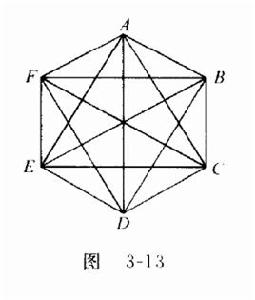
R(3,3)=6證明如下：首先，把這6個人設為A、B、C、D、E、F六個點。由A點可以引出AB、AC、AD、AE、AF五條線段。設：如果兩個人認識，則設這兩個人組成的線段為紅色；如果兩個人不認識，則設這兩個人組成的線段為藍色。
由抽屜原理可知：這五條線段中至少有三條是同色的。不妨設AB、AC、AD為紅色。若BC或CD為紅色，則結論顯然成立。若BC和CD均為藍色，則若BD為紅色，則一定有三個人相互認識；若BD為藍色，則一定有三個人互相不認識。
Ramsey數
一對常數a和b，對應於一個整數r，使得r個人中或有a個人相互認識，或有b個人互不認識；或有a個人互不認識，或有b個人相互認識。這個數r的最小值用R(a,b)來表示，也就是R(a,b)個頂點的完全圖。用紅藍兩種顏色進行著色，無論何種情況必至少存在以下兩者之一：(1)一個a個頂點著紅顏色的完全子圖，或一個b個頂點著藍顏色的完全子圖；(2)一個a個頂點著藍顏色的完全子圖，或一個b個頂點著紅顏色的完全子圖。
上述問題可以看作是R(3,3)=6的一個特例，上面的證明利用圖的形象而直觀的特點，證明了R(3,3)=6。
下面不用圖給出R(3,3)=6的證明：
對於A以外的5個人可分為Friend和Strange兩個集合。
Friend=其餘5人中與A互相認識的集合；
Strange=其餘5人中與A互相不認識的集合。
根據抽屜原理，Friend和Strange中有一個集合至少有3個人，不妨假設是集合Friend。
Friend中3個人P,Q,R若是彼此互相不認識，則問題已得到證明。否則有兩個人互相認識，不妨設這兩個人是P和Q，則A，P，Q這3個人彼此認識。
若是集合Strange至少有3個人，可以同樣討論如下：若Strange有3人L，M，N彼此互相認識，則問題的條件已得到滿足。否則設L和M互不相識，則A，L，M互不相識。
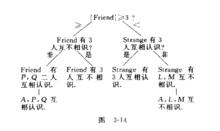Ramsey定理可以把推理過程形象地表示，如圖所示：
雖然R(3,3)的證明十分巧妙，但是實際上已知的Ramsey數非常少，比如R(3,3)=6，R(3,4)=9，R(4,4)=18保羅·艾狄胥曾以一個故事來描述尋找拉姆齊數的難度：
“想像有隊外星人軍隊在地球降落，要求取得R(5,5)的值，否則便會毀滅地球。在這個情況，我們應該集中所有電腦和數學家嘗試去找這個數值。若它們要求的是R(6,6)的值，我們要嘗試毀滅這班外星人了。”
Ramsey證明，對於給定的正整數數k及l，R(k,l)的答案是唯一和有限的。目前的進展如下圖所示（很多只有一個範圍）：
ramsey數更一般的Ramsey數
若把以上討論中紅、藍兩種顏色改為k種顏色c1,c2,...,ck，把存在a條邊的同色完全圖，或b條邊的同色完全圖，改為或a1,或a2,...，或a條邊的同色完全圖，即得到Ramsey數R(a1,a2,...,ak)，即對r個頂點的完全圖，用k種顏色c1,c2,...,ck任意染色，必然是或出現以c1顏色的a1個頂點的完全圖,或出現以c2顏色的a2個頂點的完全圖，...,或出現以ck顏色的ak個頂點的完全圖，這樣的整數r的最小值用R(a1,a2,...ak)表示。
針對Ramsey定理擴展到任意多種顏色的情況，我們給出一個非常簡略的介紹。如果n1，n2和n3都是大於或等於2的整數，則存在整數p，使得Kp→Kn1，Kn2，Kn3。
也就是說，如果把Kp的每條邊著上紅色、藍色或綠色，那么或者存在一個紅Kn1，或者存在一個藍Kn2，或者存在一個綠Kn3。使該結論成立的最小整數p稱為Ramsey數r(n1，n2，n3)。已知這種類型的僅有的非平凡Ramsey數為r(3，3，3)=17。
因此，K17→K3，K3，K3，而K16→K3，K3，K3。我們可以用類似的方法定義Ramsey數r(n1，n2，…，nk)，而對於點對Ramsey定理的完全一般形式是這些數存在；即存在整數p，使得Kp→Kn1，Kn2，…，Knk成立。
Ramsey定理還有更一般的形式，在這種形式中點對（兩個元素的子集）換成了t個元素的子集，其中t≥1是某個整數。令Ktn表示n元素集合中所有t個元素的子集的集合。將上面的概念擴展，Ramsey定理的一般形式可敘述如下：
給定整數t≥2及整數q1，q2，…，qk≥t，存在一個整數p，使得Ktp→Ktq1，Ktq2，…，Ktqk成立。也就是說，存在一個整數p，使得如果給p元素集合中的每一個t元素子集指定k種顏色c1，c2，…，ck中的一種，那么或者存在q1個元素，這些元素的所有t元素子集都被指定為顏色c1，或者存在q2個元素，這些元素的所有t元素子集都被指定為顏色c2，…，或者存在qk個元素，它的t元素子集都被指定為顏色ck。這樣的整數中最小的整數p為Ramsey數rt(q1，q2，…，qk)。
假設t=1。於是，r1(q1，q2，…，qk)就是滿足下麵條件的最小的數p：如果p元素集合的元素被用顏色c1，c2，…，ck中的一種顏色著色，那么或者存在q1個都被著成顏色c1的元素，或者存在q2個都被著成顏色c2的元素，…，或者存在qk個都被著成顏色ck的元素。因此，根據鴿巢原理的加強版，有r1(q1，q2，…，qk)=q1+q2+…+qk-k+1這就證明Ramsey定理是鴿巢原理的加強版的擴展。
確定一般的Ramsey數rt(q1，q2，…，qk)是一個困難的工作。關於它們的準確值我們知道得很少。但不難看出，rt(t，q2，…，qk)=rt(q2，…，qk)並且q1，q2，…，qk的排列順序不影響Ramsey數的值。
若干推論
（1）對6個頂點的完全圖的邊用紅、藍二色任意著色，結果至少有兩個同色的三角形。
（2）證明9個人中若不是3個人互不認識，則必有4個人互相認識，同樣，10個人中若不是3個人互相認識，則必有4個人互不認識。
（3）18個人中至少有4個人或互相認識或互相不認識。
相關定理
定理1R(a,b)=R(b,a), R(a,2)=a
定理2對任意整數a,b>=2, R(a,b)存在。
定理3對所有的整數a,b
R(a,b)<=R(a-1,b)+R(a,b-1)
定理4對所有的整數a和b，a,b>=2，若R(a,b-1)和R(a-1,b)是偶數，則
R(a,b)<=R(a-1,b)+R(a,b-1)-1
定理5對於a,b>=2,有
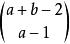Ramsey定理R(a,b)<=
註：關於以上推論和定理的證明，可以參考《組合數學（第4版）》盧開澄、盧華明編著，其中的第3章第15節給與了證明 。
