簡介
存在性定理是一類定性描述。
要把某種離散對象按某個確定的約束條件進行安排,如果這種特定的安排是否存在還不確定,就需要首先討論這種特定安排的存在性問題。在經典組合數學中,霍爾定理、拉姆齊定理和狄爾沃斯定理是三個主要的存在性定理。
內容
霍爾定理
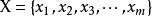 存在性定理
存在性定理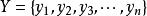 存在性定理
存在性定理霍爾定理 使用於組合問題中;二部圖G中的兩部分頂點組成的集合分別為X, Y, , ,G中有一組無公共點的邊,一端恰好為組成X的點的充分必要條件是: X中的任意k個點至少與Y中的k(1≤k≤m)個點相鄰。
霍爾定理還有一個重要推論:二部圖G中的兩部分頂點組成的集合分別為X,Y, 若∣X∣=∣Y∣,且G中有一組無公共端點的邊,一端恰好組成X中的點,一端恰好組成Y中的點, 則稱二部圖G中存在完美匹配。若圖G的每個點度數為t,則稱二部圖G為t-正則的二部圖存在完美匹配。
本定理是二分圖匹配問題中匈牙利算法的基礎。
拉姆齊定理
在組合數學上,拉姆齊(Ramsey)定理是要解決以下的問題:要找這樣一個最小的數 n,使得 n個人中必定有 k個人相識或 l個人互不相識。
6 個人中至少存在3人相互認識或者相互不認識。
該定理等價於證明這6個頂點的完全圖的邊,用紅、藍二色任意著色,必然至少存在一個紅色邊三角形,或藍色邊三角形。
狄爾沃斯定理
(Dilworth's theorem)
狄爾沃斯定理亦稱偏序集分解定理,是關於偏序集的極大極小的定理,該定理斷言:對於任意有限偏序集,其最大反鏈中元素的數目必等於最小鏈劃分中鏈的數目。此定理的對偶形式亦真,它斷言:對於任意有限偏序集,其最長鏈中元素的數目必等於其最小反鏈劃分中反鏈的數目,由偏序集P按如下方式產生的圖G稱為偏序集的可比圖:G的節點集由P的元素組成,而e為G中的邊,僅當e的兩端點在P中是可比較的,有限全序集的可比圖為完全圖。
