定義
Q檢驗法又叫做捨棄商法,是迪克森(W.J.Dixon)在1951年專為分析化學中少量觀測次數(n<10)提出的一種簡易判據式。
按以下步驟來確定可疑值的取捨:
(1)將各數據按遞增順數排列:X1,X2,X3,…,Xn-1,Xn。
(2)求出最大值與最小值的差值(極差)Xmax-Xmin.
(3)求出可疑值與其最相鄰數據之間的差值的絕對值。
(4)求出Q(Q等於(3)中的差值除以(2)中的極差)。
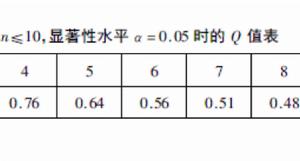
(5)根據測定次數n和要求的置信水平(如95%)查表(見下)得到值
(6)判斷:若計算Q>Q表,則捨去可疑值,否則應予保留。
| 測定次數n | Q(90%) | Q(95%) | Q(99%) |
| 3 | 0.90 | 0.97 | 0.99 |
| 4 | 0.76 | 0.84 | 0.93 |
| 5 | 0.64 | 0.73 | 0.82 |
| 6 | 0.56 | 0.64 | 0.74 |
| 7 | 0.51 | 0.59 | 0.68 |
| 8 | 0.47 | 0.54 | 0.63 |
| 9 | 0.44 | 0.51 | 0.60 |
| 10 | 0.41 | 0.49 | 0.57 |
舉例
現場儀器測在同一點上4次測出:0.1014,0.1012,0.1025,0.1016,其中0.1025與其他數值差距較大,是否應該捨去?
根據“Q值檢驗法”:
(1)對數據進行從小到大排列:0.1012,0.1014,0.1016,0.1025;
(2)求出最大值與最小值的差值=0.1025-0.1012=0.0013
(3)求出可疑數據與其相鄰數值的差值的絕對值=0.1025-0.1016=0.0009
(4)計算Q1=0.0009/0.0013=0.692
(5)測試次數為4,置信水平為0.9時的Q2=0.76
(6)由於Q1<Q2,所以,0.1025不應捨棄。