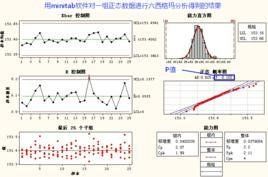
意義
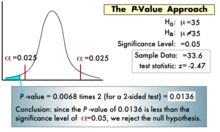P valueP值（P value）就是當原假設為真時所得到的樣本觀察結果或更極端結果出現的機率。如果P值很小，說明原假設情況的發生的機率很小，而如果出現了，根據小機率原理，我們就有理由拒絕原假設，P值越小，我們拒絕原假設的理由越充分。總之，P值越小，表明結果越顯著。但是檢驗的結果究竟是“顯著的”、“中度顯著的”還是“高度顯著的”需要我們自己根據P值的大小和實際問題來解決。
由來
R·A·Fisher（1890-1962）作為一代假設檢驗理論的創立者，在假設檢驗中首先提出P值的概念。他認為假設檢驗是一種程式，研究人員依照這一程式可以對某一總體參數形成一種判斷。也就是說，他認為假設檢驗是數據分析的一種形式，是人們在研究中加入的主觀信息。（當時這一觀點遭到了Neyman-Pearson的反對，他們認為假設檢驗是一種方法，決策者在不確定的條件下進行運作，利用這一方法可以在兩種可能中作出明確的選擇，而同時又要控制錯誤發生的機率。這兩種方法進行長期且痛苦的論戰。雖然Fisher的這一觀點同樣也遭到了現代統計學家的反對，但是他對現代假設檢驗的發展作出了巨大的貢獻。）Fisher的具體做法是：
假定某一參數的取值。
選擇一個檢驗統計量(例如z 統計量或Z 統計量) ，該統計量的分布在假定的參數取值為真時應該是完全已知的。
從研究總體中抽取一個隨機樣本計算檢驗統計量的值計算機率P值或者說觀測的顯著水平，即在假設為真時的前提下，檢驗統計量大於或等於實際觀測值的機率。
如果P<0.01，說明是較強的判定結果，拒絕假定的參數取值。
如果0.01<0.05，說明較弱的判定結果，拒絕假定的參數取值。
如果P值>0.05，說明結果更傾向於接受假定的參數取值。
可是，那個年代，由於硬體的問題，計算P值並非易事，人們就採用了統計量檢驗方法，也就是我們最初學的t值和t臨界值比較的方法。統計檢驗法是在檢驗之前確定顯著性水平α，也就是說事先確定了拒絕域。但是，如果選中相同的α，所有檢驗結論的可靠性都一樣，無法給出觀測數據與原假設之間之間不一致程度的精確度量。只要統計量落在拒絕域，假設的結果都是一樣，即結果顯著。但實際上，統計量落在拒絕域不同的地方，實際上的顯著性有較大的差異。
因此，隨著計算機的發展，P值的計算不再是個難題，使得P值變成最常用的統計指標之一。
計算
為理解P值的計算過程，用Z表示檢驗的統計量，ZC表示根據樣本數據計算得到的檢驗統計量值。
左側檢驗 H0:μ≥μ0 vs H1:μ<μ0>μ0
P值是當μ=μ0時，檢驗統計量小於或等於根據實際觀測樣本數據計算得到的檢驗統計量值的機率，即p值 = P(Z≤ZC|μ=μ0)
右側檢驗 H0:μ≤μ0 vs H1:μ>μ0
P值是當μ=μ0時，檢驗統計量大於或等於根據實際觀測樣本數據計算得到的檢驗統計量值的機率，即p值 = P(Z≥ZC|μ=μ0)
雙側檢驗 H0:μ=μ0 vs H1:μ≠μ0
P值是當μ=μ0時，檢驗統計量大於或等於根據實際觀測樣本數據計算得到的檢驗統計量值的機率，即p值 = 2P(Z≥|ZC||μ=μ0)
