適用條件:
1 隨機項存在一階序列相關
2 解釋變數與隨機項不相關,即不存在異方差
3 樣本容量比較大
檢驗步驟
提出零假設和備選假設
H0:P=0 隨機誤差項不存在一階序列相關
H1:P≠0
構造D-W檢驗統計量
D=2(1-P)
P→0時 D→2
P→1時 D→0
P→-1時 D→4
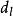 D-W檢驗
D-W檢驗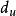 D-W檢驗
D-W檢驗杜賓和瓦特森根據樣本容量N和解釋變數數目K,在給定顯著性水平下,建立D-W檢驗統計量的下臨界值和上臨界值 ,確定了具體的用於判斷的範圍。
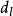 D-W檢驗
D-W檢驗0→ 正序列相關
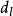 D-W檢驗
D-W檢驗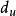 D-W檢驗
D-W檢驗→ 不確定
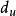 D-W檢驗
D-W檢驗→2 無序列相關
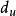 D-W檢驗
D-W檢驗2→4-無序列相關
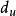 D-W檢驗
D-W檢驗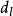 D-W檢驗
D-W檢驗4-→4- 不確定
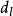 D-W檢驗
D-W檢驗4-→4 負相關 具體值在D-W表中查
解釋:該統計量的取值在0-4之間,例如如果自變數數小於4個,統計量大於2,基本上可肯定殘差間相互獨立。
局限性
只適合於一階情形
不適用於同時存在異方差和序列相關模型
存在兩個不能確定的區域
當解釋變數中含有被解釋變數的滯後項時,檢驗失效
DW分布的蒙特卡羅模擬結果
類 型 樣本容量 百 分 位 數 均 值 標準差 偏 度 JB統計量
1 90 95 99
10 0.22 2.18 2.45 2.81 1.28 0.62 0.50 48.74
DW(1,1) 20 0.11 1.28 1.49 1.80 0.75 0.39 0.68 77.61
30 0.09 0.90 1.04 1.39 0.51 0.29 1.07 293.73
40 0.06 0.77 0.88 1.16 0.41 0.25 1.06 250.10
50 0.05 0.59 0.71 0.98 0.33 0.20 1.16 341.31
10 0.18 1.73 2.02 2.38 0.98 0.53 0.73 89.59
20 0.09 1.02 1.21 1.59 0.56 0.34 1.22 369.61
DW(1,0) 30 0.06 0.70 0.83 1.18 0.38 0.24 1.27 430.43
40 0.04 0.54 0.66 0.91 0.30 0.19 1.25 383.68
50 0.04 0.45 0.54 0.71 0.24 0.15 1.12 261.84
DW(0,0) 10 1.31 2.75 2.97 3.24 2.02 0.57 0.00 7.17
40 0.72 2.41 2.53 2.70 2.00 0.31 0.03 4.06
註:
1. DW(1,1)表示由兩個I(1)變數進行回歸,計算得到的DW值。
2. DW(1,0)表示由一個I(1)變數和一個I(0)變數進行回歸,計算得到的DW值。
3. DW(0,0)表示由兩個I(0)變數進行回歸,計算得到的DW值。
4. 在每個樣本容量條件下各模擬1000次。
