0—1分布

0—1分布就是n=1情況下的二項分布。即只先進行一次事件試驗，該事件發生的機率為p，不發生的機率為1-p。這是一個最簡單的分布，任何一個只有兩種結果的隨機現象都服從0-1分布。

基本信息

• 中文名：0—1分布

• 領域：數學
• 別稱：兩點分布
• 記法：X~B(x,p)

定義

設離散型隨機變數的分布律為

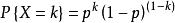0—1分布

,其中k=0,1。p為k=1時的機率(0<p<1)，則稱X服從0-1分布，0-1分布又叫 兩點分布，記為：X~B(x,p)

數學上與之相關的另一種分布即：伯努利試驗(二項分布) ：

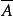0—1分布

0—1分布

如果隨機試驗E滿足：將一個試驗在相同條件下重複進行n次，各次試驗僅有兩個結果A和 ，事件A的機率在各次試驗中保持不變，P(A)=p，P( )=1-p； 各次試驗的結果互不影響，則稱隨機試驗E為n次伯努利試驗。

分布律

一個隨機事件X，X發生記為X=1，X不發生記為X=0，若事件X服從0-1分布，則X的分布律為：

X	0	1
p	1-p	p

性質

數學期望：E(X)=p

方差：D(X)=p(1-p)

舉例

即只先進行一次事件試驗，該事件發生的機率為p，不發生的機率q=1-p。這是一個最簡單的分布，任何一個只有兩種結果的隨機現象，比如，拋硬幣觀察正反面，新生兒是男還是女，檢查產品是否合格等，都可用它來描述。