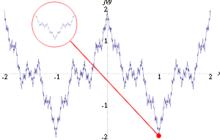
構造
在魏爾斯特拉斯的原始文獻中，這個函式定義為一個傅立葉級數：
魏爾斯特拉斯函式
魏爾斯特拉斯函式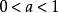
魏爾斯特拉斯函式其中 ， 為正奇數，使得：
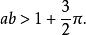魏爾斯特拉斯函式 魏爾斯特拉斯函式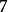
魏爾斯特拉斯函式滿足這個限制條件的 的最小值是 。這個函式的構造以及它處處連續而又處處不可導的證明首次出現於魏爾斯特拉斯於1872年6月18日在普魯士科學院提交的一篇論文中。
魏爾斯特拉斯函式
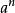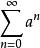魏爾斯特拉斯函式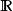
魏爾斯特拉斯函式 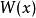魏爾斯特拉斯函式
魏爾斯特拉斯函式
魏爾斯特拉斯函式 魏爾斯特拉斯函式 魏爾斯特拉斯函式證明這個函式處處連續並不困難。由於無窮級數的函式項 的絕對值不大於常數 ，而正項級數 是收斂的，由魏爾斯特拉斯判別法可知，這個函式項級數一致收斂。又由於每一個函式項 都是 上的連續函式，所以級數和 也是 上的連續函式。不僅如此，由於每一項都是一致連續的，所以 也是一致連續的。
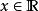魏爾斯特拉斯函式
魏爾斯特拉斯函式
魏爾斯特拉斯函式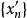
魏爾斯特拉斯函式證明函式處處不可導的思路是：對任意點 ，都能找出趨於 的兩個不同的數列 和 ，使得
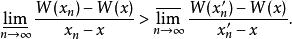魏爾斯特拉斯函式這與函式可導的定義矛盾。
一般人在直覺上會認為連續的函式必然是可導的，即使不可導，不可導的點也必然只占整體的一小部分（例如是可數集或零測集）。根據魏爾斯特拉斯的論文，之前的數學家，包括高斯，通常都是這樣假定的。這可能是因為直觀上很難想像一個連續但在不可數個點上不可導的函式。只有對於性質良好的函式，例如利普希茨函式，不可導的點才一定是零測集。
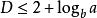魏爾斯特拉斯函式魏爾斯特拉斯函式可以說是第一個分形函式，儘管這個名詞當時還不存在。將魏爾斯特拉斯函式在任一點放大，所得到的局部圖都和整體圖形相似。無論如何放大，函式圖像都不會顯得更加平滑，不像可導函式那樣越來越接近直線；仍然具有無限的細節，不存在單調的區間。函式圖像的豪斯多夫維數 ，並且普遍認為等號總是成立的，但這還沒有得到嚴格證明。
性質
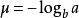魏爾斯特拉斯函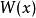式 魏爾斯特拉斯函式
魏爾斯特拉斯函式
魏爾斯特拉斯函式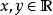
魏爾斯特拉斯函式魏爾斯特拉斯函式不是利普希茨連續的，但可以是赫爾德連續的。設 ，則 具有指數為 的赫爾德連續性，即存在常數 ，使得對任意的 都有
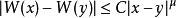魏爾斯特拉斯函式推廣
在實分析中，凡具有和魏爾斯特拉斯的原始定義相似的構造與性質的函式，都可稱為魏爾斯特拉斯函式。
本華·曼德博（Benoit Mandelbrot）給出的推廣具有形式：
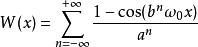魏爾斯特拉斯函式
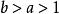魏爾斯特拉斯函式其中 。這個推廣的函式同樣是處處連續但處處不可導。此外還具有精確的自相似性，滿足重整化群方程
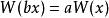魏爾斯特拉斯函式
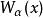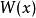魏爾斯特拉斯函式 魏爾斯特拉斯函式
魏爾斯特拉斯函式雖然沒有通常的導數，但這個函式可以有分數階導數。定義 為 的 次黎曼-劉維爾分數階導數，則有重整化群關係
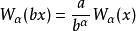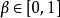魏爾斯特拉斯函式
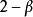魏爾斯特拉斯函式
魏爾斯特拉斯函式
魏爾斯特拉斯函式這個函式是赫爾德連續的，赫爾德指數 。有猜想認為其圖像的豪斯多夫維數就是 ，並且具有階數小於 的連續的分數階導數。
