概念
高程控制網中各待定點相對於該網已知點的高程中誤差,稱相應待定點的高程中誤差。一個待定點相對於另一個待定點的高程中誤差,稱相對高程中誤差。
測量規範中,對點位(高程)及相對點位(高程)中誤差都有若干明確的規定和要求;《城市測量規範》要求四等網最弱相鄰點的相對點位中誤差不得超過5cm,四等以下最弱點點位中誤差在1:500圖中不得超過5cm,小於1:500圖不得超過10cm,圖根點相對於圖根起算點的點位中誤差不得大於圖上0.1mm,各等水準網最弱點高程中誤差不得超過2cm,圖根點相對於圖根起算點的高程中誤差,不得大於測圖基本等高距的十分之一。《地籍測量規範》要求相鄰基本控制點的相對點位中誤差不得超過圖上0.05mm,地籍圖根控制點相對鄰近基本控制點的點位中誤差不得超過圖上0.1mm。《地質礦產勘查測量規範》要求各等級三角點的相鄰點相對點位中誤差不大於0.1m,圖根點對最近的基本控制點的平面位置中誤差應不大於0.1mm,各等級水準網,測距高程網最弱點高程中誤差應不大於0.05m。
採樣數據及柵格尺寸對高程中誤差的影響分析
研究背景
柵格DEM的水平解析度對地形分析的結果有著重要影響。因此,如何科學合理地確定柵格DEM的解析度,也就成了許多研究者關心的焦點。儘管很多研究者都對確定DEM解析度的方法進行了研究,但仍然有許多問題並未明確。例如,參與建立DEM的原始數據點的數量會對DEM的質量有怎樣的影響?建立DEM的原始數據密度與解析度的選擇有沒有聯繫?針對我國DEM的主要生產方式———全數字航空攝影測量,樣本數據密度對DEM質量影響的研究較少。試圖通過對全數字航空攝影測量所得的高精度高程數據進行分析處理,探討在建立ANUDEM和基於TIN方法的DEM(簡稱為TINDEM)時,數據密度及柵格尺寸與高程中誤差的關係。
研究方法
(1)研究區域與基礎數據
 圖1 原始數據( 局部)
圖1 原始數據( 局部)研究區位於陝北黃土丘陵溝壑區,總面積約為22.2km 。研究區域溝壑縱橫,地形複雜,高程在1000~1300m之間,平均坡度約為16°。研究所採用的原始數據是利用全數字航空攝影測量的方法,基於地面解析度0.36m的數碼航空像片建立立體量測模型進行採集的地形特徵點、線數據(見圖1)。總計採集具有高程的點數據210至225個(包含地形特徵線上的點)。原始數據格式為MicroStation的dgn格式。
(2)實驗方法
為了獲取建立DEM的不同密度的源數據,對原始數據進行以下步驟的處理:①將dgn數據轉換為dxf格式。②將dxf檔案中記錄的全部高程點和地形特徵線上的點的x、y坐標和高程值z寫入一個點文本檔案。③對該點檔案中點的數量進行抽稀。具體做法為:首先,將整個研究區域的數據劃分為10×10的格線,將距離格線中心點最近的點抽取出來作為檢校點;然後,對剩餘的數據繼續用n×n的格線劃分(n為50,100,150,200,250,300,350,400),並抽取距離格線中心點最近的點,這樣就獲得了用於計算高程中誤差的94個檢測點以及具有9種不同密度的點數據(見表1)。④利用上述9種不同密度的點數據生成不同柵格尺寸的ANUDEM和TINDEM,命名為方式A(T)DEMn-r。其中,A表示ANUDEM,T表示TINDEM,n表示數據密度系列(n=1,2,…,9),r表示柵格尺寸,r=0.3125×2n(n=0,1,2,…,9,對於ANUDEM,n=1,2,…,9)。⑤利用上述得到的檢測點和DEM數據,利用式(1)計算高程中誤差,用來分析數據密度對DEM的影響:
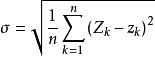 高程中誤差
高程中誤差研究結論
(1)如果要得到中誤差水平在2m左右的DEM,對於ANUDEM,參與生成DEM的數據點密度至少要大於7000個/km ,而對於TIN-DEM,則至少要大於8500個/km ,同時建立的DEM的柵格尺寸要小於5m。
(2)當柵格尺寸小於20m時,且數據密度介於7000~9400個/km 之間時,無論是ANU-DEM還是TINDEM,高程中誤差處於一個較為穩定的狀態,數據密度對高程中誤差的影響較小。
(3)相對於用TIN方法建立DEM而言,在較粗的柵格尺寸水平上(大於或等於10m),從高程中誤差水平來看,ANUDEM並不優於TIN-DEM。但當柵格尺寸較為精細時(小於10m),ANUDEM使用較少的源數據點,就可以達到TINDEM在使用更多的源數據點時的高程中誤差水平。
(4)無論建立哪種DEM,柵格尺寸並不是越小,其高程中誤差就越低。對於ANUDEM而言,其柵格尺寸下限約為2.5m,而TINDEM則在0.625m左右。
上述結論均是僅從高程中誤差的角度分析得到的,儘管高程中誤差的這種分析方法是我國評價DEM質量的基本標準,但已有學者對此種方法的可靠性提出了質疑。同時,本文建立DEM時完全使用點數據,與實際生產中建立DEM的方法有一定差距。另外,本文的研究區域為黃土丘陵溝壑區,地形較為複雜。在討論數據密度與柵格尺寸對於高程中誤差的影響時,地形複雜程度是一個需要認真考慮的因素,在不同的地形條件下,本文結論的通用性仍需進一步探討。
方格網法土石方計算與高程中誤差關係的探討
土石方計算與高程中誤差關係
土石方是現代工程建設的重要內容,是工程造價計算的關鍵步驟和環節;其計算數據的可靠性直接影響工程造價的預算,從而影響到工程建設的質量和進度。方格網法原理簡單,方便快捷,為廣大測繪工作者所推崇。但其計算精度受地形、採樣間距、測量點高程中誤差、測區面積、平均填(挖)高度、高程點密度等因素的影響。正確掌握各影響因素與土石方計算相對誤差之間的關係,便於在作業過程中採用相應的措施提高土石方計算精度。
計算原理
方格網法採用一定邊長的正方形相連組成一個方格網,覆蓋整個測區。用方格網四個角點高程和平場之間的高差計算方格內的挖方和填方的土石方量,所有計算範圍內的方格累加獲得該地塊的挖(填)方的總土石方量。
根據測區範圍布設正方格網。方格網採樣間距通常根據地形複雜度、地形圖比例尺、施工精度等要求而定。根據地形圖等高線,線性內插出方格頂點的自然地面高程。
方格網法計算結論
方格網法通常是利用研究區現有的地形圖來布置方格網,方格頂點的高程依地形圖高程而定;測量點的高程精度和密度決定了等高線的詳實情況,亦直接決定了地形圖的高程精度,是方格網法土石方精度的關鍵因素。正確掌握測量點高程中誤差與土石方精度相對誤差之間的關係,便於在測量的過程中採取有效措施,限制誤差,提高土石方計算精度,更好地為工程建設服務。