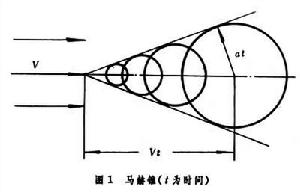
馬赫波
這是奧地利物理學家、哲學家E.馬赫在 19世紀 80年代末期90年代初期做超音速彈丸實驗時首先發現的。無論氣體靜止還是運動，微弱擾動的傳播速度相對於氣體而言必是音速。位置固定的擾源在速度超過音速（V＞a）的氣流中所發出的一個個擾動隨氣流以V的速度向下游移去,同時擾動本身又以音速a 向四面八方傳播，結果擾動所能播及的區域必限於圖1中圓錐區域以內,這圓錐是一系列擾動球面的包絡面，稱為馬赫錐。圓錐的半頂角μ＝arcsin(1/M),稱為馬赫角；M＝V/a，稱為馬赫數。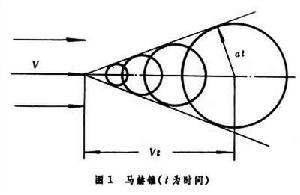
馬赫波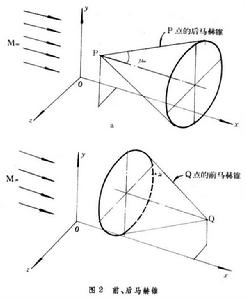
中的 P點）產生的擾動所能達到的地方，是以該點為頂點向後伸的馬赫錐以內的區域。錐的半頂角μ∞＝arc sin(a∞/ V∞)。這個V∞是來流速度（即飛行速度）,a∞是來流中的音速，這個馬赫錐稱為P點的後馬赫錐。錐內的區域稱為P點的影響所及區。反過來說,在流場上任意一點（圖2b中的Q點）所能接受到的擾動，其源也只限於一個圓錐以內。它是以 Q為頂點向前伸的馬赫錐，錐的軸線平行於來流，半頂角還是μ∞。這個馬赫錐稱為 Q的前馬赫錐。錐內的區域稱為Q點的依賴區，因為Q點的流動情況只為前馬赫錐中的擾動所決定。 參考書目
奧斯瓦梯許著，徐華舫譯：《氣體動力學》，科學出版社，北京，1965。（K. Oswatitsch, Gas Dynamics,Academic Press,New York,1956.）
