香農第一定理
香農第一定理(可變長無失真信源編碼定理)
設離散無記憶信源X包含N個符號{x1,x2,…,xi,..,xN}，信源發出K重符號序列，則此信源可發出N^k個不同的符號序列訊息，其中第j個符號序列訊息的出現機率為PKj，其信源編碼後所得的二進制代碼組長度為Bj，代碼組的平均長度B為
B=PK1B1+PK2B2+…+PKN^kBN^k
當K趨於無限大時，B和信息量H(X)之間的關係為B/k=H(X)(K趨近無窮）
香農第一定理又稱為無失真信源編碼定理或變長碼信源編碼定理。
香農第一定理的意義：將原始信源符號轉化為新的碼符號，使碼符號儘量服從等概分布，從而每個碼符號所攜帶的信息量達到最大，進而可以用儘量少的碼符號傳輸信源信息。
香農第二定理
香農第二定理（有噪信道編碼定理）
有噪信道編碼定理。當信道的信息傳輸率不超過信道容量時，採用合適的信道編碼方法可以實現任意高的傳輸可靠性，但若信息傳輸率超過了信道容量，就不可能實現可靠的傳輸。
設某信道有r個輸入符號，s個輸出符號，信道容量為C，當信道的信息傳輸率R<C，碼長N足夠長時，總可以在輸入的集合中(含有r^N個長度為N的碼符號序列)，找到M （(M<=2^(N(C-a)))，a為任意小的正數)個碼字，分別代表M個等可能性的訊息，組成一個碼以及相應的解碼規則,使信道輸出端的最小平均錯誤解碼機率Pmin達到任意小。
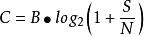香農三大定理公式：註：B為信道頻寬；S/N為信噪比，通常用分貝（dB）表示。
香農第三定理
香農第三定理（保失真度準則下的有失真信源編碼定理）
保真度準則下的信源編碼定理，或稱有損信源編碼定理。只要碼長足夠長，總可以找到一種信源編碼，使編碼後的信息傳輸率略大於率失真函式，而碼的平均失真度不大於給定的允許失真度，即D'<=D.
設R(D)為一離散無記憶信源的信息率失真函式，並且選定有限的失真函式，對於任意允許平均失真度D>=0，和任意小的a>0，以及任意足夠長的碼長N，則一定存在一種信源編碼W，其碼字個數為M<=EXP{N[R(D)+a]}，而編碼後碼的平均失真度D'(W)<=D+a。
