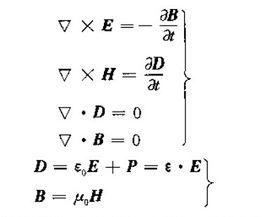常數特性
非線性極化率是非線性光學中的重要常數。由它的對稱性和大小可預測各種非線性光學效應的許多特性。例如,由其二階非線性極化率為零的性質即可斷言,各向同性介質或具有中心對稱的晶體,不存在任何二階非線性光學效應。
演算方法
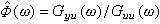 非線性光學極化率
非線性光學極化率設有l個光波作用於介質,其頻率分別為ω1、ω2、…、ωl,其偏振方向分別為α1、α2、…、αl (其中任一αi可以是x、y、z),則所產生的頻率為 ωo=ω1+ω2+…+ωl
的l階極化強度應與上述l個光波的電場成正比。該比例關係可由下式表達式中
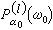 非線性光學極化率
非線性光學極化率是該極化強度的αo分量的復振幅;
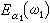 非線性光學極化率
非線性光學極化率分別為上述 l個光波電場的復振幅。式中的比例係數
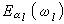 非線性光學極化率
非線性光學極化率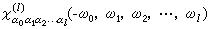 非線性光學極化率
非線性光學極化率稱為l 階非線性極化率。
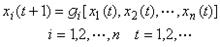 非線性光學極化率
非線性光學極化率這種複雜的標誌方式意味著它的數值既與介質有關,又與作用的光波頻率有關,還與各個光波的偏振方向以及極化強度的不同分量有關。事實上,由上述頻率成分的光波還可以產生頻率為這些頻率的其他和差組合的 l階極化。如果認為上面那些表達式中的任一ωi(i=1,2,…,l) 均既可取其真正頻率的正值也可取其負值,且認為
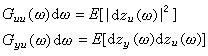 非線性光學極化率
非線性光學極化率(*號表示復共軛),則上述關係式仍可用以表達這種頻率為作用光波頻率的和差組合的極化強度。而且,其中的
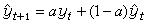 非線性光學極化率
非線性光學極化率就是相應於該頻率組合的l階非線性極化率。這樣,一般說來,非線性極化率的數值就不僅與各個作用光波的頻率有關,而且與其和差組合的形式有關。例如,兩個頻率不同的光波,其和頻極化率與差頻極化率一般是不同的。
由於
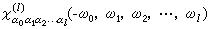 非線性光學極化率
非線性光學極化率共有l+1個角標,每一個角標αi(i=0,1,…,l)又可取三個值x、y和z,故l階非線性極化率是一個三維l+1階張量,共有
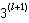 非線性光學極化率
非線性光學極化率個張量元。
非線性極化率
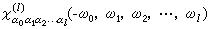 非線性光學極化率
非線性光學極化率是物質的一個常數。不同張量元之間往往有一定的關係,稱為張量元之間具有一定的對稱性。已知,非線性極化率張量元之間有兩種類型的對稱性。一類是與物質的空間對稱性無關的固有置換對稱性。例如,α1、α2 …αl中的任意兩個角標αα與αb互換,與此同時相應地ωα與ωb互換,
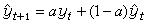 非線性光學極化率
非線性光學極化率的值不變。當所有頻率都落在非線性晶體的同一透明區時所具有的克蘭曼全對稱性也屬這類。這指的是當αo與α1、α2 …αl中的任一αα互換的同時,-ωo也與ωα互換,則
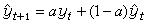 非線性光學極化率
非線性光學極化率的值也不變。另一類對稱性是與物質的空間對稱性有關的對稱性。也就是說,具有某種確定空間對稱性的介質,其非線性極化率張量元之間也必然有某種確定的關係,這種關係只與介質的空間對稱性有關,與介質的其他性質無關。因而,只要其空間對稱性相同,不論是何種介質,這種關係都是一樣的。例如,各向同性介質或具有中心對稱的晶體,二階非線性極化率均為零。又例如,各向同性介質的三階非線性極化率張量元共有243個元素,但只有以下一些張量元不為零:
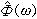 非線性光學極化率
非線性光學極化率(其中i=x、y、z,j=x、y、z)。而且它們之間存在以下確定的關係:
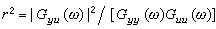 非線性光學極化率
非線性光學極化率因此,實際上獨立的張量元只有三個。
考慮到在非線性晶體的透明區,二階非線性極化率
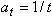 非線性光學極化率
非線性光學極化率往往與頻率的關係不大並因而交換j、k兩角標時其值不變,故有時也可將其中的角標(j,k)用一個約化指標m來表示。其對應關係為
 非線性光學極化率
非線性光學極化率這樣變更後的
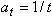 非線性光學極化率
非線性光學極化率表示為d
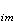 非線性光學極化率
非線性光學極化率(i=1,2,3,m=1,2,3,4,5,6),並可將其排列成一個長方形矩陣
dij習慣上稱為非線性係數。
由二階非線性係數還可派生出倍頻係數、有效非線性係數等物質常數。這些常數與二階非線性係數都有直接的對應關係。但在分析晶體的光學倍頻、混頻等效應時用起來更方便。