光學倍頻

光學倍頻

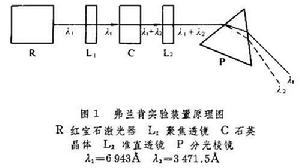
又稱光學二次諧波，是指由於光與非線性媒質（一般是晶體）相互作用,使頻率為ω的基頻光轉變為2ω的倍頻光的現象。這是一種常見而重要的二階非線性光學效應。雷射出現後的1961年，P.A.弗蘭肯等人首次利用石英晶體將紅寶石雷射器發出的波長為 694.3納米的雷射轉變成波長為347.15納米的倍頻雷射，從而開始了非線性光學的主要歷史階段。圖1是該實驗裝置的原理圖。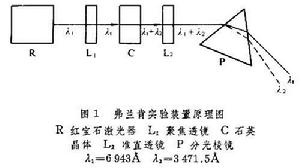

光學倍頻

光學倍頻來源於媒質在基頻光波電場作用下產生的二階非線性極化，即極化強度中與光波電場二次方成比例的部分。這一部分極化強度相當於存在一種頻率為2ω的振盪電偶極矩。基頻光波在媒質中傳播的同時激勵起一系列這樣的振盪電偶極矩。它們在空間中的分布就好比一個按一定規則排列的偶極矩陣列，偶極矩之間有一定的相對位相。由於陣列中每個電偶極矩都要輻射頻率為2ω的光波, 故偶極矩陣列的輻射應是這些光波互相干涉的結果。無疑，只當干涉是相互加強時才會有效地產生倍頻光輸出。為此,陣列中各振盪電偶極矩間要保持恰當的位相關係。 從此便產生了所謂位相匹配條件k(2ω)=2k(ω),它是產生光學倍頻的重要條件,其中k(ω)和k(2ω)分別為基頻和倍頻光在媒質中的波矢。 當這兩個光波沿同一方向傳播時，此條件轉化為要求媒質中倍頻光的折射率n(2ω)等於基頻光的折射率n(ω)。

位相匹配

例如，對於負單軸晶體，在正常色散情況下，可選擇光的偏振方向使基頻光為尋常光，倍頻光為非常光，再通過夾角θ 來實現位相匹配。參看圖2,其中的圓（球面）是頻率為ω 的尋常光的折射率曲面。它表示這種光在任意方向傳播時折射率n(ω)均等於n憙 。該圖的橢圓(橢球面)是頻率為 2ω 的非常光的折射率曲面。它表示這種光的折射率n(2ω)隨傳播方向θ而變化, 在最大值n厺與最小值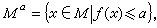之間沿著橢圓變動。當θ=θm時球面與橢球面相交，即光沿此方向傳播時n(ω)＝n(2ω)。這意味著當選擇此方向入射基頻光時，位相匹配條件得到滿足並在同一方向會有倍頻光輸出。

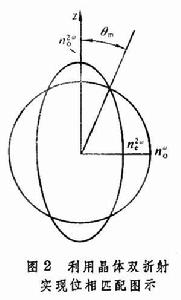光學倍頻

當滿足位相匹配條件時，倍頻光功率密度正比於基頻光功率密度的二次方，也正比於晶體作用長度的二次方。此外還與媒質的倍頻係數（二階非線性極化率）二次方成正比。
光學倍頻可將紅外雷射轉變為可見雷射，或將可見雷射轉變為波長更短的雷射，從而擴展雷射譜線覆蓋的範圍。在雷射技術中已被廣泛採用。為得到波長更短的雷射可用多級倍頻。

多種倍頻晶體

且可達到相當高的倍頻轉換效率。對於可見及近紅外的基頻光，常用的倍頻晶體有 KDP、KD*P、ADP、LiIO3、CDA等等, 轉換效率可高達30％～50％。對於中紅外基頻光,常用晶體為Ag3AsS3、GdGeAs2、Te、CdSe等，轉換效率為5％～15％左右。
參考書目
　P. A. Franken, et al., Generation of Optical Harmonics, Phys.Rev. Lett.,Vol.7,p.118,1961.
　F.Zernike,J.Midwinter,Applied Nonlinear Optics，John Wiley & Sons, New York, 1973.

配圖

相關連線