非空二叉樹

至少有一個結點的二叉樹叫做非空二叉樹。二叉樹是每個節點最多有兩個子樹的樹結構。 樹是由n（n>=1）個有限節點組成一個具有層次關係的集合。它具有以下的特點： 每個節點有零個或多個子節點；沒有父節點的節點稱為根節點；每一個非根節點有且只有一個父節點；除了根節點外，每個子節點可以分為多個不相交的子樹。

基本形態

非空二叉樹是遞歸定義的，其結點有左右子樹之分，邏輯上非空二叉樹有四種基本形態：

(1)只有一個根結點的二叉樹

(2)只有左子樹

(3)只有右子樹

(4)完全二叉樹

類型

非空二叉樹主要有以下三種類型：

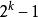非空二叉樹

滿二叉樹——一棵深度為k的且有個結點的二叉樹叫滿二叉樹。

特點：每一層上的結點數都是最大結點數。

平衡二叉樹——平衡二叉樹又被稱為AVL樹（區別於AVL算法），它是一棵二叉排序樹，且具有以下性質：它是一棵空樹或它的左右兩個子樹的高度差的絕對值不超過1，並且左右兩個子樹都是一棵平衡二叉樹。

完全二叉樹——深度為k，有n個結點的二叉樹若且唯若其每一個結點都與深度為k的滿二叉樹中編號從1至n的結點一一對應時，稱為完全二叉樹。

特點：葉子結點只可能在層次最大的兩層上出現。 對任一結點，若其右分支下子孫的最大層次為L，則其左分支下子孫的最大層次必為L或L+1。

性質

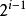非空二叉樹

在非空二叉樹中，第i層的結點總數不超過, i>=1；

對任何非空二叉樹T，若n0 表示葉結點的個數、n2 表示度為2 的非葉結點的個數，那么兩者滿足關係n0 = n2 + 1。