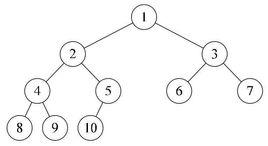
定義
若設二叉樹的深度為h，除第 h 層外，其它各層 (1～h-1) 的結點數都達到最大個數，第 h 層所有的結點都連續集中在最左邊，這就是完全二叉樹。
完全二叉樹是由滿二叉樹而引出來的。對於深度為K的，有n個結點的二叉樹，若且唯若其每一個結點都與深度為K的滿二叉樹中編號從1至n的結點一一對應時稱之為完全二叉樹。
(1)所有的葉結點都出現在第k層或k-l層（層次最大的兩層）
(2)對任一結點，如果其右子樹的最大層次為L，則其左子樹的最大層次為L或L+l。
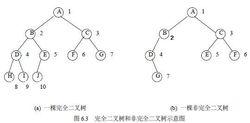完全二叉樹與非完全二叉樹一棵二叉樹至多只有最下面的兩層上的結點的度數可以小於2，並且最下層上的結點都集中在該層最左邊的若干位置上，則此二叉樹成為完全二叉樹，並且最下層上的結點都集中在該層最左邊的若干位置上，而在最後一層上，右邊的若干結點缺失的二叉樹，則此二叉樹成為完全二叉樹。
性質
如果一棵具有n個結點的深度為k的二叉樹，它的每一個結點都與深度為k的滿二叉樹中編號為1~n的結點一一對應，這棵二叉樹稱為完全二叉樹。
可以根據公式進行推導，假設n是度為0的結點總數（即葉子結點數），n是度為1的結點總數，n是度為2的結點總數，則 ：
①n= n+n+n（其中n為完全二叉樹的結點總數）；又因為一個度為2的結點會有2個子結點，一個度為1的結點會有1個子結點，除根結點外其他結點都有父結點，
②n= 1+n+2*n；由①、②兩式把n消去得：n= 2*n+n-1，由於完全二叉樹中度為1的結點數只有兩種可能0或1，由此得到n=n/2 或 n=(n+1)/2。
簡便來算，就是 n=n/2，其中n為奇數時（n=0）向上取整；n為偶數時（n=1）。可根據完全二叉樹的結點總數計算出葉子結點數。
特點
葉子結點只可能在最大的兩層上出現,對任意結點，若其右分支下的子孫最大層次為L，則其左分支下的子孫的最大層次必為L 或 L+1；
出於簡便起見,完全二叉樹通常採用數組而不是鍊表存儲,其存儲結構如下:
var tree:array[1..n]of longint;{n:integer;n>=1}
對於tree[i] ，有如下特點：
（1）若i為奇數且i>1，那么tree的左兄弟為tree[i-1]；
（2）若i為偶數且i<n，那么tree的右兄弟為tree[i+1]；
（3）若i>1，tree的父親節點為tree[i div 2]；
（4）若2*i<=n，那么tree的左孩子為tree[2*i]；若2*i+1<=n，那么tree的右孩子為tree[2*i+1]；
（5）若i>n div 2,那么tree[i]為葉子結點（對應於（3））；
（6）若i<(n-1) div 2.那么tree[i]必有兩個孩子（對應於（4））。
（7）滿二叉樹一定是完全二叉樹，完全二叉樹不一定是滿二叉樹。
完全二叉樹第i層至多有2^（i-1）個節點，共i層的完全二叉樹最多有2^i-1個節點。
完全二叉樹的特點是：
1）只允許最後一層有空缺結點且空缺在右邊，即葉子結點只能在層次最大的兩層上出現；
2）對任一結點，如果其右子樹的深度為j，則其左子樹的深度必為j或j+1。 即度為1的點只有1個或0個
完全二叉樹判定
算法思路
判斷一棵樹是否是完全二叉樹的思路
1>如果樹為空，則直接返回錯
2>如果樹不為空：層序遍歷二叉樹
2.1>如果一個結點左右孩子都不為空，則pop該節點，將其左右孩子入佇列；
2.1>如果遇到一個結點，左孩子為空，右孩子不為空，則該樹一定不是完全二叉樹；
2.2>如果遇到一個結點，左孩子不為空，右孩子為空；或者左右孩子都為空；則該節點之後的佇列中的結點都為葉子節點；該樹才是完全二叉樹，否則就不是完全二叉樹；
