內容簡介
在使用擴展先序遍歷創建二叉樹時，首先要根據一棵二叉樹寫出它的先序遍歷序列，然後根據圖中各個節點左右孩子的 狀況進行加點遍歷，凡是沒有左右孩子的節點，遍歷到它的左右孩子是都用“.”表示它的左右孩子，注意這裡面的“.”只是用來表示它的父節點沒有它這個左孩子或右孩子，並不表示節點，所以在遍歷過程中應該訪問到“.”就結束了，不能再沿著“.”繼續遍歷。
基本內容
所謂遍歷(Traversal)是指沿著某條搜尋路線，依次對樹中每個結點均做一次且僅做一次訪問。訪問結點所做的操作依賴於具體的套用問 題。 遍歷是二叉樹上最重要的運算之一，是二叉樹上進行其它運算之基礎。本節主要講二叉樹中遍歷過程，遍歷方法，重點介紹擴展先序遍歷序列以及利用此序列創建二叉樹的過程，順便比較一下各種遍歷方法的異同和套用。
先序遍歷
從二叉樹的遞歸定義可知，一棵非空的二叉樹由根結點及左、右子樹這三個基本部分組成。因此，在任一給定結點上，可以按某種次序執行三個操作：
（1）訪問結點本身(N)，
（2）遍歷該結點的左子樹(L)，
（3）遍歷該結點的右子樹(R)。
根據遍歷的原則：先左後右，對於先序遍歷，顧名思義就是先訪問根節點，再訪問左子樹，最後訪問右子樹，
中序遍歷
從二叉樹的遞歸定義可知，一棵非空的二叉樹由根結點及左、右子樹這三個基本部分組成。因此，在任一給定結點上，可以按某種次序執行三個操作：
（1）遍歷該結點的左子樹(L)，
（2）訪問結點本身(N)，
（3）遍歷該結點的右子樹(R)。
對於中序遍歷，就是先訪問左子樹，再訪問根節點，最後訪問右子樹；
後序遍歷
從二叉樹的遞歸定義可知，一棵非空的二叉樹由根結點及左、右子樹這三個基本部分組成。因此，在任一給定結點上，可以按某種次序執行三個操作：
（1）遍歷該結點的左子樹(L)，
（2）遍歷該結點的右子樹(R)。
（3）訪問結點本身(N)，
對於後序遍歷，就是先訪問左子樹，再訪問右子樹，最後訪問根節點；
遍歷的命名
根據訪問結點操作發生位置命名：
① NLR：前序遍歷(PreorderTraversal亦稱(先序遍歷))
——訪問根結點的操作發生在遍歷其左右子樹之前。
② LNR：中序遍歷(InorderTraversal)
——訪問根結點的操作發生在遍歷其左右子樹之中(間)。
③ LRN：後序遍歷(PostorderTraversal)
——訪問根結點的操作發生在遍歷其左右子樹之後。
算法實現
先序遍歷的算法實現
用二叉鍊表做為存儲結構，先序遍歷算法可描述為：
void InOrder(BinTree T)
{ //算法里①~⑥是為了說明執行過程加入的標號
① if(T) { // 如果二叉樹非空
② printf("%c"，T->data)； // 訪問結點 ③ InOrder(T->lchild)； ④ InOrder(T->rchild); ⑤ }
⑥ } // InOrder
擴展先序遍曆法創建二叉樹算法實現
void createBiTree(BiTree *bt){
char ch;
ch = getchar();
if(ch == '.')
*bt = NULL;
else{
*bt = (BiTree)malloc(sizeof(BiTNode));//向記憶體申請節點空間
(*bt)->data = ch;
createBiTree(&((*bt)->LChild));//生成左子樹
createBiTree(&((*bt)->RChild));//生成右子樹
}
}/*createBiTree*/
列印二叉樹算法實現
/*==================列印二叉樹=============*/
void printTree(BiTree bt,int nLayer){
int i;
if(bt == NULL)
return ;
printTree(bt ->RChild,nLayer+1);
for(i=0;i<nLayer;i++)
printf(" ");
printf("%c\n",bt->data);
printTree(bt->LChild,nLayer+1);
}
輸入示例
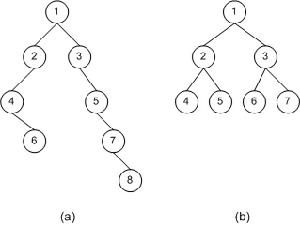
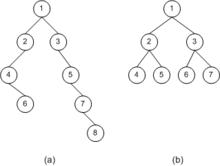擴展先序遍歷序列圖一：擴展先序遍歷序列：
(a)1 2 4 . 6 . . . 3 . 5 . 7 . 8 . .
(b)1 2 4 . . 5 . . 3 6 . . 7 . .
圖二：
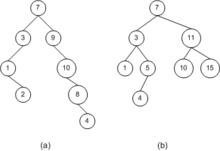擴展先序遍歷序列擴展先序遍歷序列：
(a)7 3 1 . 2 . . . 9 . 10 . 8 . 4 . .
(b)7 3 1 . . 5 4 . . . 11 10 . . 15 . .
