詞語簡介
基本意義
遍:全面,到處;如遍布、遍及、遍野、普遍。
 遍歷
遍歷歷:行、遊歷、週遊
伏軾撙銜,橫歷天下。——《戰國策》
歷聘(遊歷天下以求聘用);歷國(遊歷各國);歷行(遍行,走遍);歷塊(穿過一國如過一小塊土地);歷說(遊說)
詳細釋義
遍歷就是全部走遍,到處週遊的意思;
示例
遍歷名山,博採方術。——前蜀· 杜光庭《李筌》
宋 陸游 《舟中曉賦》詩:“高檣健席從今始,遍歷三湘與五湖。”
清 戴名世 《自序》:“自燕逾濟 ,游於渤海之濱,遍歷齊魯之境。”
釋玄奘,陳留人。貞觀三年出關西行,遍歷諸國;
(鄭和)自蘇州劉家河泛海至福建,復自福建五虎門揚帆,首達占域,以次遍歷諸國"。
辨析
古文中還有一種遍歷的用法:如:乃以是履棄之於道旁,即遍歷人家捕之,若有女履者,捕之以告。
這裡的遍是全面、到處的意思;而歷,在這裡應當作逐一、逐個地的來講。
所以這裡的遍歷的意思是全部逐一的;
二叉樹
方案
從二叉樹的遞歸定義可知,一棵非空的二叉樹由根結點及左、右子樹這三個基本部分組成。
 遍歷
遍歷因此,在任一給定結點上,可以按某種次序執行三個操作:
⑴訪問結點本身(N),
⑵遍歷該結點的左子樹(L),
⑶遍歷該結點的右子樹(R)。
以上三種操作有六種執行次序:
NLR、LNR、LRN、NRL、RNL、RLN。
注意:
前三種次序與後三種次序對稱,故只討論先左後右的前三種次序。
命名
根據訪問結點操作發生位置命名:
① NLR:前序遍歷(PreorderTraversal亦稱(先序遍歷))
——訪問結點的操作發生在遍歷其左右子樹之前。
② LNR:中序遍歷(InorderTraversal)
——訪問結點的操作發生在遍歷其左右子樹之中(間)。
③ LRN:後序遍歷(PostorderTraversal)
——訪問結點的操作發生在遍歷其左右子樹之後。
注意:
由於被訪問的結點必是某子樹的根,所以N(Node)、L(Left subtree)和R(Right subtree)又可解釋為根、根的左子樹和根的右子樹。NLR、LNR和LRN分別又稱為先根遍歷、中根遍歷和後根遍歷。
遍歷算法
中序
若二叉樹非空,則依次執行如下操作:
⑴遍歷左子樹;
⑵訪問根結點;
⑶遍歷右子樹。
先序
若二叉樹非空,則依次執行如下操作:
⑴ 訪問根結點;
⑵ 遍歷左子樹;
⑶ 遍歷右子樹。
後序
若二叉樹非空,則依次執行如下操作:
⑴遍歷左子樹;
⑵遍歷右子樹;
⑶訪問根結點。
中序算法
用二叉鍊表做為存儲結構,中序遍歷算法可描述為:
void InOrder(BinTree T)
{ //算法里①~⑥是為了說明執行過程加入的標號
① if(T) { // 如果二叉樹非空
② InOrder(T->lchild);
③ printf("%c",T->data); // 訪問結點
④ InOrder(T->rchild);
⑤ }
⑥ } // InOrder
序列
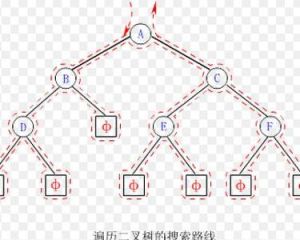
1.遍歷二叉樹的執行蹤跡
三種遞歸遍歷算法的搜尋路線相同(如下圖虛線所示)。
具體線路為:
從根結點出發,逆時針沿著二叉樹外緣移動,對每個結點均途徑三次,最後回到根結點。
2.遍歷序列
⑴ 中序序列
中序遍歷二叉樹時,對結點的訪問次序為中序序列
【例】中序遍歷上圖所示的二叉樹時,得到的中序序列為:
D B A E C F
⑵ 先序序列
先序遍歷二叉樹時,對結點的訪問次序為先序序列
【例】先序遍歷上圖所示的二叉樹時,得到的先序序列為:
A B D C E F
⑶ 後序序列
後序遍歷二叉樹時,對結點的訪問次序為後序序列
【例】後序遍歷上圖所示的二叉樹時,得到的後序序列為:
D B E F C A
注意
⑴ 在搜尋路線中,若訪問結點均是第一次經過結點時進行的,則是前序遍歷;若訪問結點均是在第二次(或第三次)經過結點時進行的,則是中序遍歷(或後序遍歷)。只要將搜尋路線上所有在第一次、第二次和第三次經過的結點分別列表,即可分別得到該二叉樹的前序序列、中序序列和後序序列。
⑵ 上述三種序列都是線性序列,有且僅有一個開始結點和一個終端結點,其餘結點都有且僅有一個前趨結點和一個後繼結點。為了區別於樹形結構中前趨(即雙親)結點和後繼(即孩子)結點的概念,對上述三種線性序列,要在某結點的前趨和後繼之前冠以其遍歷次序名稱。
【例】上圖所示的二叉樹中結點C,其前序前趨結點是D,前序後繼結點是E;中序前趨結點是E,中序後繼結點是F;後序前趨結點是F,後序後繼結點是A。但是就該樹的邏輯結構而言,C的前趨結點是A,後繼結點是E和F。
二叉鍊表的構造
1. 基本思想 基於先序遍歷的構造,即以二叉樹的先序序列為輸入構造。
注意:
先序序列中必須加入虛結點以示空指針的位置。
【例】
建立上圖所示二叉樹,其輸入的先序序列是:ABD∮∮CE∮∮F∮∮。
2. 構造算法
假設虛結點輸入時以空格字元表示,相應的構造算法為:
void CreateBinTree (BinTree *T)
{ //構造二叉鍊表。T是指向根指針的指針,故修改*T就修改了實參(根指針)本身
char ch;
if((ch=getchar())=="") *T=NULL; //讀入空格,將相應指針置空
else{ //讀入非空格
*T=(BinTNode *)malloc(sizeof(BinTNode)); //生成結點
(*T)->data=ch;
CreateBinTree(&(*T)->lchild); //構造左子樹
CreateBinTree(&(*T)->rchild); //構造右子樹
}
}
注意:調用該算法時,應將待建立的二叉鍊表的根指針的地址作為實參。
圖
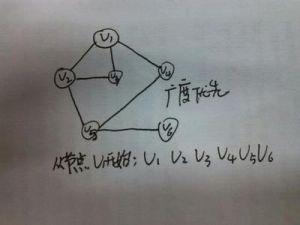
深度優先
(Depth-First Traversal)
圖的深度優先遍歷的遞歸定義:
假設給定圖G的初態是所有頂點均未曾訪問過。在G中任選一頂點v為初始出發點(源點),則深度優先遍歷可定義如下:首先訪問出發點v,並將其標記為已訪問過;然後依次從v出發搜尋v的每個鄰接點w。若w未曾訪問過,則以w為新的出發點繼續進行深度優先遍歷,直至圖中所有和源點v有路徑相通的頂點(亦稱為從源點可達的頂點)均已被訪問為止。若此時圖中仍有未訪問的頂點,則另選一個尚未訪問的頂點作為新的源點重複上述過程,直至圖中所有頂點均已被訪問為止。
圖的深度優先遍歷類似於樹的前序遍歷。採用的搜尋方法的特點是儘可能先對縱深方向進行搜尋。這種搜尋方法稱為深度優先搜尋(Depth-First Search)。相應地,用此方法遍歷圖就很自然地稱之為圖的深度優先遍歷。
深度優先搜尋的過程
設x是當前被訪問頂點,在對x做過訪問標記後,選擇一條從x出發的未檢測過的邊(x,y)。若發現頂點y已訪問過,則重新選擇另一條從x出發的未檢測過的邊,否則沿邊(x,y)到達未曾訪問過的y,對y訪問並將其標記為已訪問過;然後從y開始搜尋,直到搜尋完從y出發的所有路徑,即訪問完所有從y出發可達的頂點之後,才回溯到頂點x,並且再選擇一條從x出發的未檢測過的邊。上述過程直至從x出發的所有邊都已檢測過為止。此時,若x不是源點,則回溯到在x之前被訪問過的頂點;否則圖中所有和源點有路徑相通的頂點(即從源點可達的所有頂點)都已被訪問過,若圖G是連通圖,則遍歷過程結束,否則繼續選擇一個尚未被訪問的頂點作為新源點,進行新的搜尋過程。
算法實現