離散函式

定義域是離散集合的函式，稱為離散函式。其定義域和值域都可以是任意集合。研究中主要分為二大類：有限集與可列集。

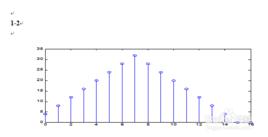
離散函式：定義域是離散集合的函式稱為離散函式。其函式圖像為一系列離散的點。

研究中根據離散函式的定義域主要分有二大類：有限集與可列集。

有限集：基數為有限個數的集合。（屬於自然數集的真子集）

若定義域和值域都為有限集，其研究研究的主要理論依據為鴿洞原理（對一個非一對一函式充分性的判別）。

可列集(enumerable)：與自然數集等勢的集合，即可以與自然數集進行一一映射的集合（如自然數集、 有理數集、 代數數集等，但不包含實數集、複數集、直線點集、 平麵點集等）。

離散數值函式：定義域是自然數集，值域是實數域的離散函式。