簡介
用數字計算機對一個連續系統進行仿真時,必須將這個系統看作一個時間離散系統。也就是說,只能計算到各狀態量在各計算步距點上的數值,它們是一些時間離散點的數值。數值積分法沒有顯式地涉及到“離散”這個概念。史密斯從控制和工程的概念出發提出離散相似問題,並導出離散相似法。
離散相似法的基本原理
 離散相似法
離散相似法 離散相似法
離散相似法 離散相似法
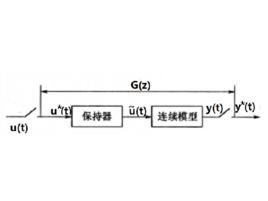
離散相似法用周期為 的虛擬採樣開關將連續模型的輸入、輸出分別離散化,要求離散化後的輸出 在採樣時刻的值等同於原輸出在同一時刻的值,以後的每一步計算均在這個模型基礎上進行,而原來的連續模型不再參與計算,如圖1所示。對比數值積分法雖然也進行了離散化處理,但在離散化過程中每一步都用到連續系統的模型(導函式 ),離散一步計算一步。
 圖1(a)
圖1(a) 圖1(b)
圖1(b)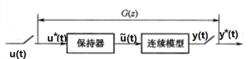 圖1(c)
圖1(c) 離散相似法
離散相似法 離散相似法
離散相似法顯然,如果僅僅對原系統的輸入、輸出加上採樣開關(圖1(b)),那么其輸出 與圖1(a)中的 是不會等同的。這是因為在圖1(b)中,在開關斷開期間,原連續系統無輸入,而只在開關閉合的瞬時才有輸人。為了原連續系統模型的輸入端總保持與圖1(a)近似的連續輸入,在採樣開關與原連續模型之間,必須加一個保持器,如圖1(c)所示,其近似程度取決於採樣周期和保持器的特性。
保持器的類型
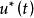 離散相似法
離散相似法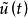 離散相似法
離散相似法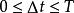 離散相似法
離散相似法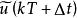 離散相似法
離散相似法保持器是把離散模擬信號 轉換成模擬信號 ,用來實現採樣點之間的插值,即要得到 時, 的值。所以保持器起了外推器的作用,外推公式為
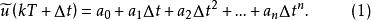 離散相似法
離散相似法上式稱為 n階外推公式,代表的是 n階保持器。
(1) 零階保持器(常值外推)。對於式(1),當n=0時,得到零階保持器的外推公式
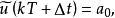 離散相似法
離散相似法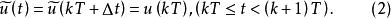 離散相似法
離散相似法零階保持器的衝激回響函式如圖2(a)所示。回響的幅值為1,寬度為T。這個特性表明零階保持器對採樣值既不放大,也不衰減,另外,也說明零階保持器只能不增不減地保持一個採樣周期。
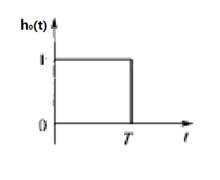 圖2(a) 零階保持器的衝激回響
圖2(a) 零階保持器的衝激回響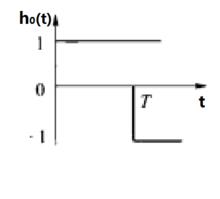 圖2(b)零階保持器的衝激回響
圖2(b)零階保持器的衝激回響對於圖2(a)特性可分解為兩個階躍函式之和,如圖2(b)所示。
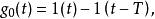 離散相似法
離散相似法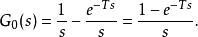 離散相似法
離散相似法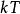 離散相似法
離散相似法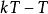 離散相似法
離散相似法(2) 一階保持器(由k-1和k外推)。在式(1)中n=1時,利用 和 時刻的值作直線外推,可得到一階保持器的外推公式:
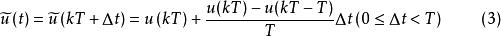 離散相似法
離散相似法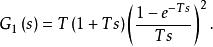 離散相似法
離散相似法(3) 滯後一步的三角形保持器。三角形保持器的計算公式為
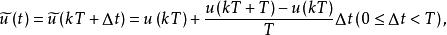 離散相似法
離散相似法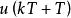 離散相似法
離散相似法因計算中用到 ,有時不方便,故用滯後一步的三角形保持器,此時有
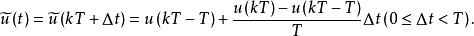 離散相似法
離散相似法傳遞函式為
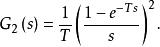 離散相似法
離散相似法由於連續系統的數學模型可以用傳遞函式來表示,也可以用狀態空間模型來表示,因此,與連續系統相似的離散模型可以通過兩個途徑獲得。其一是對傳遞函式作離散化處理得到 Z傳遞函式,稱為 Z域離散相似法;其二是基於狀態空間方程離散化,得到時域離散相似模型。
Z域離散相似法
Z域離散相似法的系統脈衝傳遞函式
 離散相似法
離散相似法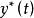 離散相似法
離散相似法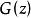 離散相似法
離散相似法在圖1(c)中,從 到 之間的傳遞函式為 ,即
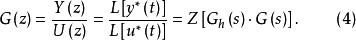 離散相似法
離散相似法 離散相似法
離散相似法對式(4)取Z逆變換即可得到關於的差分方程。
Z域離散相似法的步驟
離散相似法的步驟如下:
(1)畫出連續系統的結構圖;
(2)在適當的地方引入虛擬採樣開關,選擇合適的信號保持器;
(3)將所引進的信號保持器傳遞函式與連續系統傳遞函式串聯,通過Z變換求得系統的Z傳遞函式;
(4)通過Z逆變換得系統的差分方程,即離散模型;
(5)根據差分方程編制仿真程式。
離散相似法的精度與穩定性
離散相似模型只能等效於原來的連續系統,其精度與穩定性受採樣周期和信號保持器性能的影響。
1)採樣周期的影響
為使G(s)與G(z)等價,採樣周期T應滿足採樣定理(香農定理),即
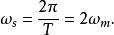 離散相似法
離散相似法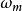 離散相似法
離散相似法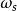 離散相似法
離散相似法式中: 為輸入信號的最高頻率; 為採樣頻率。
可以證明,若採樣周期T滿足採樣定理,且保持器為理想保持器,則輸入信號經保持器後可無失真地恢復原信號,加到原連續系統的輸人端;否則(即不滿足採樣定理或不是理想的保持器),原連續系統輸入信號失真,計算結果必然產生誤差,且採樣周期越大,誤差越大。
2)保持器的影響
(1)零階保持器。能將階躍輸入的採樣值完全恢復為階躍信號,不產生計算方法上的誤差。但隨著輸入信號頻率的增加,零階保持器的相位滯後增加,幅頻特性衰減,保持器的輸出將失真。如果系統環節較多,離散時又採用零階保持器,那么零階保持器的相位滯後的累積就會使整個系統離散化模型的穩定性變差,甚至導致不穩定。對其他輸入信號,有誤差,故需減小採樣周期。
(2)一階保持器。能復現等速輸入信號和階躍信號,對其他信號會失真,相位滯後,幅值衰減。
(3)滯後一步的三角形保持器。能復現階躍信號。
因此,添加信號保持器的離散環節不宜過多,否則相位滯後,誤差增大,穩定性變差,甚至不穩定。因此,在離散化時,凡能合併為一個環節的就合併為一個環節,這樣可以改善算法的穩定性和精度。
用數字補償器提高離散相似法的精度和穩定性
由於信號保持器產生相位滯後及幅值衰減,不能精確地復現原來的信號,所以為了減少失真,常常在信號保持器後面串聯一個補償器(圖3),以彌補信號保持器所帶來的幅值衰減和相位滯後。
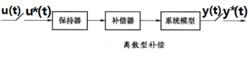 圖3
圖3其中補償器的傳遞函式為
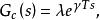 離散相似法
離散相似法 離散相似法
離散相似法 離散相似法
離散相似法式中: 為幅值補償係數; 為相位補償係數。
在實際套用中,通常取
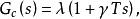 離散相似法
離散相似法 離散相似法
離散相似法 離散相似法
離散相似法可通過調整 和 來達到補償因保持器所造成的幅值衰減和相位滯後。
時域離散相似法
轉移矩陣法(時域離散相似法):如果連續系統的狀態空間模型為
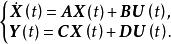 離散相似法
離散相似法式中, A、B、C、D均為常數矩陣,則同樣可以按離散相似法原理對它進行離散化處理,求得離散化狀態方程組(差分方程組)。
離散狀態空間模型
其基本思想是:先求出狀態方程的通解(解析解),進而在通解上對系統模型進行離散化處理,從而得到離散化狀態空間模型。
矩陣指數的計算
 離散相似法
離散相似法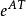 離散相似法
離散相似法利用狀態方程離散化方法時的主要問題是,如何根據具體系統計算係數矩陣。對於一些常見的一階、二階環節,通常只有一個狀態變數,此時矩陣 A變成常量,因此可方便地用解析方法求解。而對一般的高階及多輸入多輸出系統,求解 等矩陣指數函式較困難,需採用計算方法。
1)解析計算
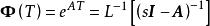 離散相似法
離散相似法利用定義 進行求解。
2)數值解法
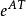 離散相似法
離散相似法求 的數值解法有很多,但常用的數值解法是基於泰勒級數展開法或精度較高的乘方與縮進法。